题目内容
已知![]() ,函数
,函数![]() ,
,![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 在区间
在区间![]() 上的最小值;
上的最小值;
(2)是否存在实数![]() ,使曲线
,使曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直? 若存在,求出
轴垂直? 若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题主要考查函数与导数等知识,考查分类讨论,化归与转化的数学思想方法,以及推理论证能力和运算求解能力)
(1)解:∵![]() ,∴
,∴![]() .
.
令![]() ,得
,得![]() .
.
①若![]() ,则
,则![]() ,
,![]()
![]() 在区间
在区间![]() 上单调递增,此时函数
上单调递增,此时函数![]() 无最小值.………2分
无最小值.………2分
②若![]() ,当
,当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以当![]() 时,函数
时,函数![]() 取得最小值
取得最小值![]() .………4分
.………4分
③若![]() ,则
,则![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以当![]() 时,函数
时,函数![]() 取得最小值
取得最小值![]() .………6分
.………6分
综上可知,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上无最小值;
上无最小值;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ;
;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .………7分
.………7分
(2)解:∵![]() ,
,![]() ,
,
∴ ![]()
![]() .………8分
.………8分
由(1)可知,当![]() 时,
时,![]() .
.
此时![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,即
,即![]() .
.
当![]() ,
,![]() ,
,![]() ,
,
∴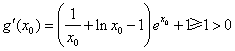 .………10分
.………10分
曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直
轴垂直
等价于方程![]() 有实数解.
有实数解.
而![]() ,即方程
,即方程![]() 无实数解.故不存在
无实数解.故不存在![]() ,使曲线
,使曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直.………14分
轴垂直.………14分

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
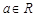 ,函数
,函数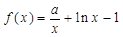 ,
,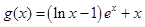 (其中
(其中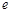 为自然对数的底数).
为自然对数的底数).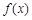 在
在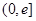 上的单调性;
上的单调性;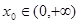 ,使曲线
,使曲线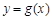 在点
在点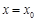 处的切线与
处的切线与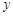 轴垂直? 若存在,
轴垂直? 若存在,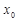 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;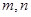 满足
满足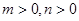 ,求证:
,求证: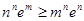 .
. ,函数
,函数 ,(其中
,(其中 为自然对数的底数).
为自然对数的底数). 在
在 上的单调性;
上的单调性; ,使曲线
,使曲线 在点
在点 处的切线与
处的切线与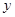 轴垂直? 若存在,求出
轴垂直? 若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.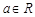 ,函数
,函数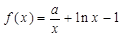 ,
,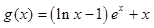 (其中
(其中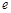 为自然对数的底数).(1)判断函数
为自然对数的底数).(1)判断函数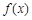 在
在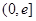 上的单调性;
上的单调性;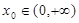 ,使曲线
,使曲线 在点
在点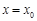 处的切线与
处的切线与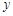 轴垂直? 若存在,
轴垂直? 若存在,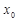 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.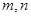 满足
满足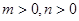 ,求证:
,求证: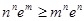 。
。 ,函数
,函数 ,
, (其中
(其中 为自然对数的底数).(1)判断函数
为自然对数的底数).(1)判断函数 在区间
在区间 上的单调性;(2)是否存在实数
上的单调性;(2)是否存在实数 ,使曲线
,使曲线 在点
在点 处的切线与
处的切线与 轴垂直? 若存在,求出
轴垂直? 若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.