题目内容
【题目】已知函数![]() .
.
(1)当![]() ,求函数
,求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(3)已知![]() ,
, ![]() ,
, ![]() 均为正实数,且
均为正实数,且![]() ,求证
,求证![]()
![]() .
.
【答案】(1) ![]() (2)
(2) ![]() (3)见解析
(3)见解析
【解析】试题分析:1)求导函数,可得切线的斜率,求出切点的坐标,可得函数y=f(x)的图象在x=0处的切线方程;
(2)先确定﹣1≤a<0,再根据函数f(x)在(0,1)上单调递增,可得f′(x)≥0在(0,1)上恒成立,构造![]() =(x+1)ln(x+1)﹣x,证明h(x)在(0,1)上的值域为(0,2ln2﹣1),即可求实数a的取值范围;
=(x+1)ln(x+1)﹣x,证明h(x)在(0,1)上的值域为(0,2ln2﹣1),即可求实数a的取值范围;
(3)由(2)知,当a=﹣1时, ![]() 在(0,1)上单调递增,证明
在(0,1)上单调递增,证明![]()
![]() ,即
,即![]()
![]() 从而可得结论.
从而可得结论.
试题解析:
(1)当![]() 时,
时, ![]() 则
则![]() ,
,
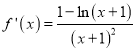 则
则![]() ,
,
∴函数![]() 的图象在
的图象在![]() 时的切线方程为
时的切线方程为![]() .
.
(2)∵函数![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() 在
在![]() 上无解,
上无解,
当![]() 时,
时, ![]() 在
在![]() 上无解满足,
上无解满足,
当![]() 时,只需
时,只需![]() ,∴
,∴![]() ①
①
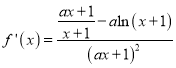 ,
,
∵函数![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立.
上恒成立.
设![]()
![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 上的值域为
上的值域为![]() .
.
∴![]() 在
在![]() 上恒成立,则
上恒成立,则![]() ②
②
综合①②得实数![]() 的取值范围为
的取值范围为![]() .
.
(3)由(2)知,当![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增,
于是当![]() 时,
时, ![]()
![]() ,
,
当![]() 时,
时, ![]()
![]() ,
,
∴![]()
![]() ,即
,即![]()
![]() ,
,
同理有![]()
![]() ,
, ![]()
![]() ,
,
三式相加得![]()
![]()
![]() .
.

练习册系列答案
相关题目