题目内容
已知函数 是
是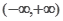 上的偶函数,若对于
上的偶函数,若对于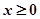 ,都有
,都有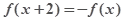 ,且当
,且当 时,
时, ,则
,则 ( )
( )
A.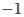 | B.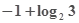 | C. | D.1 |
A
解析试题分析:因对于x≥0,都有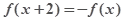 ,则
,则 ,
,
∴函数的周期为T=4,∵函数f(x)是(-∞,+∞)上的偶函数,x∈[0,2),f(x)=log2(x+1)∴ ,选A.
,选A.
考点:1.函数的奇偶性;2.函数的周期性

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知 是偶函数,它在[0,+∞)上是减函数.若
是偶函数,它在[0,+∞)上是减函数.若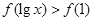 ,则x的取值范围是( )
,则x的取值范围是( )
A.(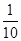 ,1) ,1) | B.(0,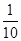 )∪(1,+∞) )∪(1,+∞) |
C.(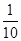 ,10) ,10) | D.(0,1)∪(10,+∞) |
函数 在
在 上为减函数,则
上为减函数,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
设偶函数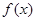 满足:当
满足:当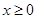 时,
时,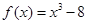 ,则
,则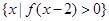 =( )
=( )
A.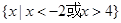 | B.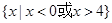 |
C.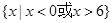 | D.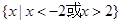 |
在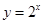 、
、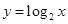 、
、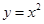 这三个函数中,当
这三个函数中,当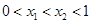 时,使
时,使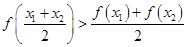 恒成立的函数个数是:( )
恒成立的函数个数是:( )
A. 0 0 | B.1 | C.2 | D.3 |
下列函数在其定义域内既是奇函数又是增函数的是( )
A. | B. | C. | D. |
椭圆 上有两个动点P、Q,E(3,0),EP
上有两个动点P、Q,E(3,0),EP EQ,则
EQ,则 的最小值为( )
的最小值为( )
| A.6 | B. | C.9 | D. |
设定义在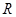 上的函数
上的函数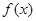 是最小正周期为
是最小正周期为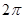 的偶函数,
的偶函数,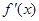 是
是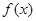 的导函数,当
的导函数,当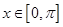 时,
时,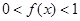 ;当
;当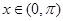 且
且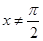 时 ,
时 ,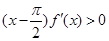 ,则函数
,则函数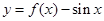 在
在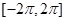 上的零点个数为( )
上的零点个数为( )
| A.2 | B.4 | C.5 | D.8 |
 上存在三点A,B,C,使得
上存在三点A,B,C,使得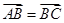 ,则称曲线有“中位点”,下列曲线
,则称曲线有“中位点”,下列曲线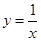 ,(3)
,(3)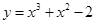 ,(4)
,(4)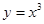 有“中位点”的是( )
有“中位点”的是( )