题目内容
已知 是偶函数,它在[0,+∞)上是减函数.若
是偶函数,它在[0,+∞)上是减函数.若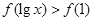 ,则x的取值范围是( )
,则x的取值范围是( )
A.(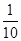 ,1) ,1) | B.(0,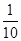 )∪(1,+∞) )∪(1,+∞) |
C.(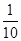 ,10) ,10) | D.(0,1)∪(10,+∞) |
C
解析试题分析:根据偶函数的性质将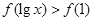 转化成
转化成 ,然后利用单调性建立不等关系,解之即可.
,然后利用单调性建立不等关系,解之即可. 是偶函数
是偶函数
 可转化成
可转化成
 在[0,+∞)上是减函数
在[0,+∞)上是减函数 即
即
 故选C
故选C
考点:复合函数的单调性;奇偶性与单调性的综合.

练习册系列答案
相关题目
为了得到函数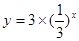 的图象,可以把函数
的图象,可以把函数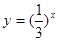 的图象( )
的图象( )
| A.向左平移3个单位长度 | B.向右平移3个单位长度 |
| C.向左平移1个单位长度 | D.向右平移1个单位长度 |
函数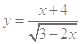 的定义域是 ( )
的定义域是 ( )
A.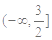 | B.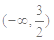 | C.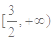 | D.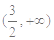 |
下列四组函数中,表示同一函数的一组是( )
A. | B.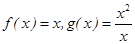 |
C.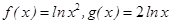 | D.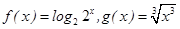 |
设 为定义在
为定义在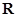 上的奇函数,当
上的奇函数,当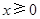 时,
时,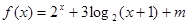 (
( 为常数),则
为常数),则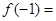 ( )
( )
A.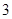 | B.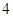 | C.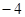 | D.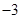 |
下列函数中,在其定义域内是增函数的为( )
A. | B. | C. | D. |
已知函数f(x)为奇函数,且当x>0时,f(x)=x2+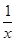 ,则f(-1)=( )
,则f(-1)=( )
| A.-2 | B.0 | C.1 | D.2 |
已知函数 是
是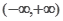 上的偶函数,若对于
上的偶函数,若对于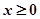 ,都有
,都有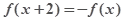 ,且当
,且当 时,
时, ,则
,则 ( )
( )
A.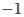 | B.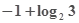 | C. | D.1 |
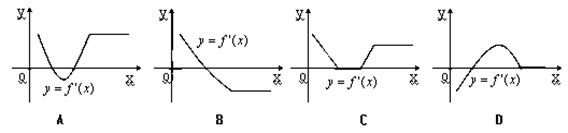
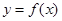 的图象如图所示,则导函数
的图象如图所示,则导函数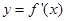 的图象的大致形状是( )
的图象的大致形状是( )