题目内容
已知函数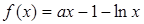
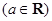 .
.
(1)当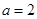 时,求函数
时,求函数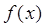 的单调区间;
的单调区间;
(2)若函数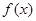 在
在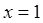 处取得极值,对
处取得极值,对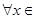
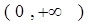 ,
,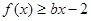 恒成立,求实数
恒成立,求实数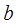 的取值范围;
的取值范围;
(3)当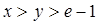 时,求证:
时,求证: .
.
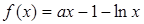
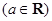 .
.(1)当
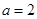 时,求函数
时,求函数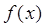 的单调区间;
的单调区间;(2)若函数
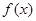 在
在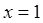 处取得极值,对
处取得极值,对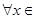
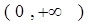 ,
,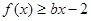 恒成立,求实数
恒成立,求实数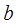 的取值范围;
的取值范围;(3)当
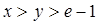 时,求证:
时,求证: .
.(1)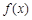 在
在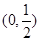 上递减,在
上递减,在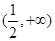 上递增;(2)
上递增;(2)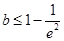 (3)
(3)
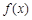 在
在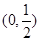 上递减,在
上递减,在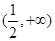 上递增;(2)
上递增;(2)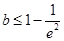 (3)
(3)试题分析:(1)
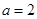 时,
时,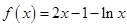 。先求导并通分整理,再令导数大于0得增区间,令导数小于0得减区间。(2)先求导,因为函数
。先求导并通分整理,再令导数大于0得增区间,令导数小于0得减区间。(2)先求导,因为函数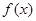 在
在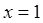 处取得极值,则
处取得极值,则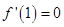 ,可得
,可得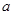 的值。对
的值。对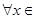
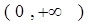 ,
,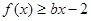 恒成立等价于
恒成立等价于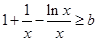 恒成立,令
恒成立,令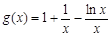 ,求导,讨论导数的符号,可得函数
,求导,讨论导数的符号,可得函数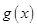 的单调性,根据单调性可得函数
的单调性,根据单调性可得函数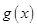 的最值,则
的最值,则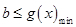 。(3)
。(3)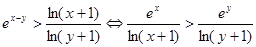 ,令
,令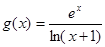 ,因为
,因为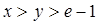 则只要证明
则只要证明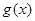 在
在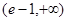 上单调递增。即证在
上单调递增。即证在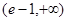 上
上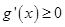 恒成立。将函数
恒成立。将函数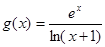 求导,分析其导数的单调性,根据其单调性求最值,证得
求导,分析其导数的单调性,根据其单调性求最值,证得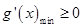 即可。
即可。(1)
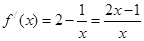
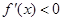 得0<x<
得0<x<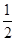 ,
,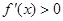 得x>
得x>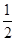
∴
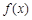 在
在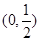 上递减,在
上递减,在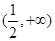 上递增.
上递增.(2)∵函数
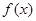 在
在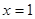 处取得极值,∴
处取得极值,∴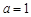 ,
, ∴
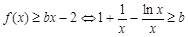 ,
, 令
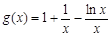 ,可得
,可得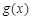 在
在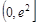 上递减,在
上递减,在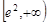 上递增,
上递增,∴
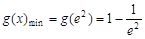 ,即
,即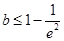 .
.(3)证明:
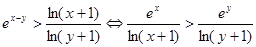 ,
,令
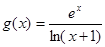 ,则只要证明
,则只要证明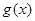 在
在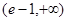 上单调递增,
上单调递增,又∵
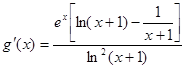 ,
,显然函数
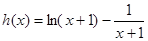 在
在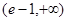 上单调递增.
上单调递增.∴
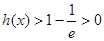 ,即
,即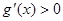 ,
,∴
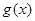 在
在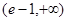 上单调递增,即
上单调递增,即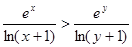 ,
,∴当
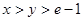 时,有
时,有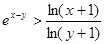 .
. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
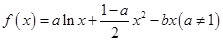 ,曲线
,曲线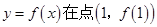 处的切线斜率为0
处的切线斜率为0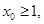 使得
使得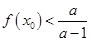 ,求a的取值范围。
,求a的取值范围。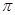 为圆周率,
为圆周率,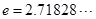 为自然对数的底数.
为自然对数的底数.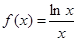 的单调区间;
的单调区间;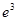 ,
,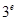 ,
,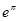 ,
,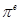 ,
,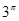 ,
,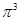 这6个数中的最大数与最小数;
这6个数中的最大数与最小数;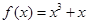 ,
,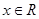 .若当
.若当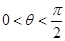 时,不等式
时,不等式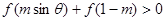 恒成立,则实数
恒成立,则实数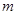 的取值范围是( )
的取值范围是( )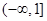
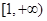
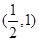
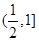
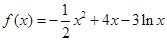 在
在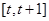 上不单调,则
上不单调,则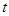 的取值范围是( )
的取值范围是( )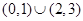
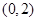
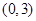
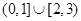
 ,函数
,函数 ,
, .
.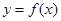 与曲线
与曲线 在它们的交点
在它们的交点 处的切线互相垂直,求
处的切线互相垂直,求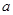 ,
, 的值;
的值; ,若对任意的
,若对任意的 ,且
,且 ,都有
,都有 ,求
,求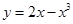 在横坐标为
在横坐标为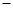 l的点处的切线为
l的点处的切线为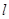 ,则直线
,则直线



 ;③(ex)′=ex;④(
;③(ex)′=ex;④( )′=x;⑤(x·ex)′=ex+1.
)′=x;⑤(x·ex)′=ex+1.