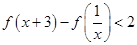题目内容

解不等式 （
1
2
）3x+2＞（
1
2
）-2x-3．
分析：由函数 y=(
1
2
)x 在R上是减函数，结合题意得 3x+2＜-2x-3，求得x的范围，即得原不等式的解集．
解答：解：由函数 y=(
1
2
)x 在R上是减函数，结合题意得 3x+2＜-2x-3，解得x＜-1．
故原不等式的解集为{x|x＜-1}，
点评：本题主要考查指数函数的单调性的应用，属于基础题．
练习册系列答案
相关题目
有下列命题：
①命题“?x∈R，使得x2+1＞3x”的否定是“?x∈R，都有x2+1≤3x”；
②设p、q为简单命题，若“p∨q”为假命题，则“￢p∧￢q为真命题”；
③若p（x）=ax2+2x+1＞0，则“?x∈R，p（x）是真命题”的充要条件为 a＞1；
④若函数f（x）为R上的奇函数，当x≥0，f（x）=3x+3x+a，则f（-2）=-14；
⑤不等式
x+5
(x-1)2
≥2的解集是[-
1
2
，3]．
其中所有正确的说法序号是
①②③④
①②③④
．
不等式10
x+5
(x-1)2
≥100的解集是（　　）

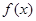（本小题12分）若是定义在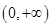上的增函数，且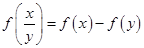 

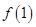（1）求的值；（2）解不等式：；

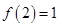（3）若，解不等式

 
有下列命题：
①命题“?x∈R，使得x2+1＞3x”的否定是“?x∈R，都有x2+1≤3x”；
②设p、q为简单命题，若“p∨q”为假命题，则“￢p∧￢q为真命题”；
③若p（x）=ax2+2x+1＞0，则“?x∈R，p（x）是真命题”的充要条件为 a＞1；
④若函数f（x）为R上的奇函数，当x≥0，f（x）=3x+3x+a，则f（-2）=-14；
⑤不等式
x+5
(x-1)2
≥2的解集是[-
1
2
，3]．
其中所有正确的说法序号是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网