题目内容
(本小题12分)若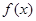 是定义在
是定义在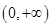 上的增函数,且
上的增函数,且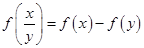
(1)求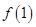 的值;(2)解不等式:
的值;(2)解不等式: ;
;
(3)若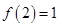 ,解不等式
,解不等式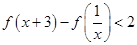
【答案】
(1)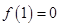 ;(2)
;(2)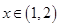 ;(3)
;(3)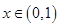 。
。
【解析】本试题主要是考查了抽象函数的性质和函数不等式的综合运用。
(1)在等式中令x=y 0,得到f(1)的值。
0,得到f(1)的值。
(2)因为 ,且又
,且又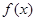 是定义在
是定义在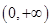 上的增函数,可知x的取值范围。
上的增函数,可知x的取值范围。
(3)故原不等式为: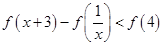
即,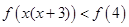
利用单调性得到结论。
解:(1)在等式中令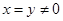 ,则
,则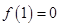 ;
;
(2)∵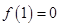

又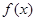 是定义在
是定义在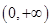 上的增函数
上的增函数

∴ 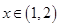
(3)故原不等式为: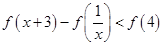
即,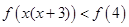
又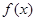 在
在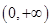 上为增函数,故原不等式等价于:
上为增函数,故原不等式等价于:
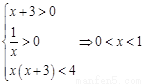

练习册系列答案
相关题目
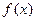 是定义在
是定义在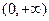 上的增函数,且对一切
上的增函数,且对一切 ,满足
,满足 .
.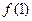 的值
的值 ,解不
,解不 等式
等式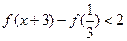 .
.
 是以原点
是以原点 为中心,以
为中心,以 、
、 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线 是以
是以 是曲线
是曲线 为钝角,若
为钝角,若 ,
, .
. 、
、 、
、 、
、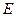 四点(如图),若
四点(如图),若 为
为 的中点,
的中点, 为
为 的中点,问
的中点,问 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由. .
.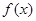 在
在 [1,+∞
[1,+∞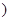 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围; 是
是