题目内容
 如图:过抛物线y2=4x上的点A(1,2)作切线l交x轴与直线x=-4分别于D,B.动点P是抛物线y2=4x上的一点,点E在线段AP上,满足
如图:过抛物线y2=4x上的点A(1,2)作切线l交x轴与直线x=-4分别于D,B.动点P是抛物线y2=4x上的一点,点E在线段AP上,满足 ;点F在线段BP上,满足
;点F在线段BP上,满足 ,3λ1+2λ2=15且在△ABP中,线段PD与EF交于点Q.
,3λ1+2λ2=15且在△ABP中,线段PD与EF交于点Q.
(1)求点Q的轨迹方程;
(2)若M,N是直线x=-3 上的两点,且⊙O1:(x+2)2+y2=1是△QMN的内切圆,试求△QMN面积的取值范围.
 解:(1)切线AB:y=x+1,D(-1,0),
解:(1)切线AB:y=x+1,D(-1,0),B(-4,-3),
 =(3,3),
=(3,3), =(2,2),
=(2,2), =
= ,
,则
 =
= ,
,令

=
 ,
,由于E,Q,F三点共线,所以
 ,
,即
 ,
,又3λ1+2λ2=15,故
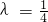 ,Q分
,Q分 的定比为
的定比为 ,
,设P(x0,y0),Q(x,y),则
 ,
,故
 ,得
,得 (y
(y )
)(2)设Q(x0,y0)(
 ),M(-3,m),N(-3,n),
),M(-3,m),N(-3,n),则
 (
( )
)切线MQ:y-m=
 ,
,由相切可得:(x0+1)m2+2y0m-(x0+3)=0,
同理(x0+1)n2+2y0n-(x0+3)=0.
知m,n是方程(x0+1)x2+2y0x-(x0+3)=0的两根
故
 ,
, ,
,
=
 ,
,令t=x0+1,
则
 (t
(t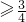 ),
),二次求导可知g′(t)>0,
△QMN面积的取值范围
 .
.分析:(1)切线AB:y=x+1,D(-1,0),B(-4,-3),
 =(3,3),
=(3,3), =(2,2),
=(2,2), =
= ,则
,则 =
= ,由此能求出点Q的轨迹方程.
,由此能求出点Q的轨迹方程.(2)设Q(x0,y0)(
 ),M(-3,m),N(-3,n),则
),M(-3,m),N(-3,n),则 (
( ).切线MQ:y-m=
).切线MQ:y-m= ,由相切可得:(x0+1)m2+2y0m-(x0+3)=0,同理(x0+1)n2+2y0n-(x0+3)=0.由此能求出△QMN面积的取值范围.
,由相切可得:(x0+1)m2+2y0m-(x0+3)=0,同理(x0+1)n2+2y0n-(x0+3)=0.由此能求出△QMN面积的取值范围.点评:本题考查点Q的轨迹方程的求法和求△QMN面积的取值范围,具体涉及到抛物线的性质、圆的性质和直线与圆锥曲线的相关知识,解题时要认真审题,仔细解答.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
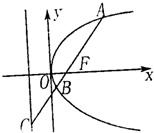 如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为 78、如图,过抛物线y2=4x的焦点F的直线交抛物线与圆(x-1)2+y2=1于A,B,C,D四点,则|AB|•|CD|=
78、如图,过抛物线y2=4x的焦点F的直线交抛物线与圆(x-1)2+y2=1于A,B,C,D四点,则|AB|•|CD|= 如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B(|AF|>|BF|),交其准线于点C,若|BC|=2|BF|,且|AF|=2,则此抛物线的方程为
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B(|AF|>|BF|),交其准线于点C,若|BC|=2|BF|,且|AF|=2,则此抛物线的方程为 如图,过抛物线y2=2px(p>0)的焦点F且倾斜角为60°的直线l交抛物线于A、B两点,若|AF|=3,则此抛物线方程为( )
如图,过抛物线y2=2px(p>0)的焦点F且倾斜角为60°的直线l交抛物线于A、B两点,若|AF|=3,则此抛物线方程为( ) 如图,过抛物线y2=4x焦点的直线依次交抛物线与圆(x-1)2+y2=1于A,B,C,D,则
如图,过抛物线y2=4x焦点的直线依次交抛物线与圆(x-1)2+y2=1于A,B,C,D,则