题目内容
椭圆与双曲线之间有许多类似的性质:
P是椭圆
+
=1(a>b>0)上任一点,焦点F1、F2,∠F1PF2=α,三角形PF1F2面积为b2
,类比,P是双曲线
-
=1(a>0,b>0)上任一点,焦点F1、F2,∠F1PF2=α,三角形PF1F2面积为
P是椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| sinα |
| 1+cosα |
| x2 |
| a2 |
| y2 |
| b2 |
b2
| sinα |
| 1-cosα |
b2
.| sinα |
| 1-cosα |
分析:类似椭圆的性质,将面积表达式的“+”号改成“-”即得b2
.设|PF1|=r1,|PF2|=r2,根据三角形面积公式可表示出△PF1F2的面积,由余弦定理可求得r1r2的表达式,进而求得S与b和tanθ的关系式,原式得证.
| sinα |
| 1-cosα |
解答:解:类似椭圆的性质:P是双曲线
-
=1(a>0,b>0)上任一点,焦点F1、F2,∠F1PF2=α,三角形PF1F2面积为 b2
.
证明:设|PF1|=r1,|PF2|=r2,
则S=
r1r2sin2θ,又|F1F2|=2c,
由余弦定理有
(2c)2=r12+r22-2r1r2cos2θ=(r1+r2)2-2r1r2-2r1r2cos2θ=(2a)2-2r1r2(1+cos2θ),
于是2r1r2(1+cos2θ)=4a2-4c2=4b2.
所以r1r2=
.
这样即有S=
•
sin2θ=b2
=b2
.
故答案为:b2
.
| x2 |
| a2 |
| y2 |
| b2 |
| sinα |
| 1-cosα |
证明:设|PF1|=r1,|PF2|=r2,
则S=
| 1 |
| 2 |
由余弦定理有
(2c)2=r12+r22-2r1r2cos2θ=(r1+r2)2-2r1r2-2r1r2cos2θ=(2a)2-2r1r2(1+cos2θ),
于是2r1r2(1+cos2θ)=4a2-4c2=4b2.
所以r1r2=
| 2b2 |
| 1+cos2θ |
这样即有S=
| 1 |
| 2 |
| 2b2 |
| 1+cos2θ |
| 2sinθcosθ |
| 2cos2θ |
| sinα |
| 1-cosα |
故答案为:b2
| sinα |
| 1-cosα |
点评:本题主要考查了圆锥曲线的共同特征.考查了学生综合分析问题和解决问题的能力,有些圆锥曲线问题用定义去解决比较方便.如本题,设|PF1|=r1,|PF2|=r2,则S=
r1r2sin2θ.若能消去r1r2,问题即获解决.
| 1 |
| 2 |

练习册系列答案
相关题目
 +
+ =1(a>b>0)上任一点,焦点F1、F2,∠F1PF2=α,三角形PF1F2面积为b2
=1(a>b>0)上任一点,焦点F1、F2,∠F1PF2=α,三角形PF1F2面积为b2 ,类比,P是双曲线
,类比,P是双曲线 的离心率为 ;若椭圆
的离心率为 ;若椭圆 与双曲线C有相同的焦点,则a= .
与双曲线C有相同的焦点,则a= .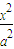 +
+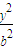 =1(a>b>0)上任一点,焦点F1、F2,∠F1PF2=α,三角形PF1F2面积为b2
=1(a>b>0)上任一点,焦点F1、F2,∠F1PF2=α,三角形PF1F2面积为b2 ,类比,P是双曲线
,类比,P是双曲线 -
-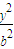 =1(a>0,b>0)上任一点,焦点F1、F2,∠F1PF2=α,三角形PF1F2面积为 .
=1(a>0,b>0)上任一点,焦点F1、F2,∠F1PF2=α,三角形PF1F2面积为 .