题目内容
在(
-
)8的展开式中,
(1)系数的绝对值最大的项是第几项?
(2)求二项式系数最大的项;
(3)求系数最大的项.
| x |
| 2 |
| x2 |
(1)系数的绝对值最大的项是第几项?
(2)求二项式系数最大的项;
(3)求系数最大的项.
考点:二项式定理的应用
专题:二项式定理
分析:(1)根据最大的系数绝对值大于等于其前一个系数绝对值;同时大于等于其后一个系数绝对值;列出不等式求出系数绝对值最大的项.
(2)利用展开式中中间项的二项式系数最大,判断出第5项的二项式系数最大;利用二项展开式的通项公式求出第5项.
(3)据系数正负交替出现,故求系数最大的项;
(2)利用展开式中中间项的二项式系数最大,判断出第5项的二项式系数最大;利用二项展开式的通项公式求出第5项.
(3)据系数正负交替出现,故求系数最大的项;
解答:
解:(1)设系数绝对值最大的项是第k+1项,于是
解得5≤k≤6,
所以k=5或k=6时系数的绝对值最大,
故系数的绝对值最大的项是第6项和第7项.
(2)二项式系数最大的项是第5项,于是T5
(
)8-4•(-2)4•x-8=
•24x-6;
(3)由(1)知,系数的绝对值最大的项是第6项和第7项.由于系数为正的项为奇数项,故第7项系数最大,
T7
•x•(-2)6•x-12=1792x-11.
|
解得5≤k≤6,
所以k=5或k=6时系数的绝对值最大,
故系数的绝对值最大的项是第6项和第7项.
(2)二项式系数最大的项是第5项,于是T5
| =C | 4 8 |
| x |
| C | 4 8 |
(3)由(1)知,系数的绝对值最大的项是第6项和第7项.由于系数为正的项为奇数项,故第7项系数最大,
T7
| =C | 6 8 |
点评:本题考查二项式系数的性质:中间项的二项式系数最大、考查二项展开式的通项公式、考查求系数最大项的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在直三棱柱ABC-A1B1C1中,D、E分别为AA1、CC1的中点,AC⊥BE,点F在线段AB上,且AB=4AF,若M为线段BE上一点,试确定M在线段BE上的位置,使得C1D∥平面B1FM.
如图,在直三棱柱ABC-A1B1C1中,D、E分别为AA1、CC1的中点,AC⊥BE,点F在线段AB上,且AB=4AF,若M为线段BE上一点,试确定M在线段BE上的位置,使得C1D∥平面B1FM.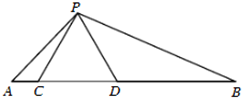 如图,点C、D在线段AB上,且△PCD是等边三角形.
如图,点C、D在线段AB上,且△PCD是等边三角形.