题目内容
设复数z1=x+yi(x,y∈R,y≠0),复数z2=cosα+isinα(α∈R),且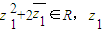 在复平面上所对应点在直线y=x上,求|z1-z2|的取值范围.
在复平面上所对应点在直线y=x上,求|z1-z2|的取值范围.
【答案】分析:先根据题中的两个条件建立方程组,解出复数z1后,化简|z1-z2|的解析式,利用正弦函数的有界性求出|z1-z2|的取值范围.
解答:解:
 ,
,
 ,∴x=y=1,∴z1=1+i,
,∴x=y=1,∴z1=1+i,
|z1-z2|= ,
,
∴|z1-z2| .
.
点评:本题考查求复数的模的方法,复数为实数的条件,三角公式的应用及正弦函数的有界性.
解答:解:

 ,
, ,∴x=y=1,∴z1=1+i,
,∴x=y=1,∴z1=1+i,|z1-z2|=
 ,
,∴|z1-z2|
 .
.点评:本题考查求复数的模的方法,复数为实数的条件,三角公式的应用及正弦函数的有界性.

练习册系列答案
相关题目
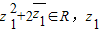 在复平面上所对应点在直线y=x上,求|z1-z2|的取值范围.
在复平面上所对应点在直线y=x上,求|z1-z2|的取值范围.