题目内容
设P在[0，5]上随机地取值，求方程x2+px+
+
=0有实根的概率
．
| p |
| 4 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 5 |
分析：由题意知方程的判别式大于等于零求出p的范围，再判断出所求的事件符合几何概型，再由几何概型的概率公式求出所求事件的概率．
解答：解：若方程x2+px+
+
=0有实根，则△=（p）2-4×（
+
）≥0，
即p2-p-2≥0，解得，m≥2或 m≤-1；
∵记事件A：设P在[0，5]上随机地取值，
由方程x2+px+
+
=0有实根符合几何概型，
∴P（A）=
=
．
故答案为：
．
| p |
| 4 |
| 1 |
| 2 |
| p |
| 4 |
| 1 |
| 2 |
即p2-p-2≥0，解得，m≥2或 m≤-1；
∵记事件A：设P在[0，5]上随机地取值，
由方程x2+px+
| p |
| 4 |
| 1 |
| 2 |
∴P（A）=
| 5-2 |
| 5 |
| 3 |
| 5 |
故答案为：
| 3 |
| 5 |
点评：本题考查了求几何概型下的随机事件的概率，即求出所有实验结果构成区域的长度和所求事件构成区域的长度，再求比值．
练习册系列答案
相关题目
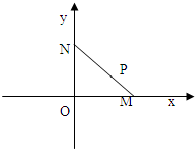如图，线段MN的两个端点M、N分别在x轴、y 轴上滑动，|MN|=5，点P是线段MN上一点，且
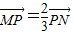，点P随线段MN的运动而变化．
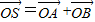，是否存在这样的直线l，使四边形OASB的对角线相等（即|OS|=|AB|）？若存在，求出直线l的方程；若不存在，试说明理由．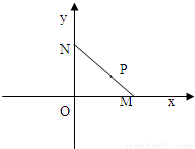
，点P随线段MN的运动而变化．
，是否存在这样的直线l，使四边形OASB的对角线相等（即|OS|=|AB|）？若存在，求出直线l的方程；若不存在，试说明理由．