题目内容
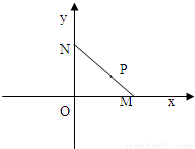
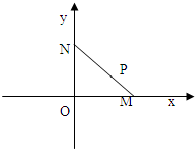 如图,线段MN的两个端点M、N分别在x轴、y 轴上滑动,|MN|=5,点P是线段MN上一点,且
如图,线段MN的两个端点M、N分别在x轴、y 轴上滑动,|MN|=5,点P是线段MN上一点,且| MP |
| 2 |
| 3 |
| PN |
(1)求点P的轨迹C的方程;
(2)过点(2,0)作直线l,与曲线C交于A、B两点,O是坐标原点,设
| OS |
| OA |
| OB |
分析:(1)用消参法求轨迹方程,可先设出M,N,P点的坐标,用M,N点的坐标表示P点坐标,再消掉参数即可.
(2)先假设存在直线l,使四边形OASB的对角线相等,四边形OASB为矩形,OA⊥OB,再设出l的方程,与(1)中所求椭圆方程联立,得到x1x2,y1y2的表达式,根据OA⊥OB,x1x2+y1y2=0,求k,若能求出,则存在,否则,不存在.
(2)先假设存在直线l,使四边形OASB的对角线相等,四边形OASB为矩形,OA⊥OB,再设出l的方程,与(1)中所求椭圆方程联立,得到x1x2,y1y2的表达式,根据OA⊥OB,x1x2+y1y2=0,求k,若能求出,则存在,否则,不存在.
解答: 解:(1)设M(x0,0),N(0,y0),P(x,y) 因为|MN|=5,所以x02+y02=25(*)
解:(1)设M(x0,0),N(0,y0),P(x,y) 因为|MN|=5,所以x02+y02=25(*)
又点P是MN上一点,且|MP|=2,所以P分
所成的比为
∴
∴
将其代入(*)得
+
=1即为所求的方程
(2)
=
+
,所以四边形OASB为平行四边形,若存在l使得|
|=|
|,则四边形OASB为矩形
∴
•
=0若l的斜率不存在,直线l的方程为x=2,由
得
∴
•
=
>0,与
•
=0矛盾,故l的斜率存在.
设l的方程为y=k(x-2),A(x1,y1),B(x2,y2)由
⇒(9k2+4)x2-36k2x+36(k2-1)=0
∴x1+x2=
,x1x2=
①
y1y2=[k(x1-2)][k(x2-2)]=k2[x1x2-2(x1+x2)+4]=-
②
把①、②代入x1x2+y1y2=0得k=±
∴存在直线l:3x-2y-6=0或3x+2y-6=0使得四边形OASB的对角线相等
 解:(1)设M(x0,0),N(0,y0),P(x,y) 因为|MN|=5,所以x02+y02=25(*)
解:(1)设M(x0,0),N(0,y0),P(x,y) 因为|MN|=5,所以x02+y02=25(*)又点P是MN上一点,且|MP|=2,所以P分
| MN |
| 2 |
| 3 |
∴
|
|
将其代入(*)得
| x2 |
| 9 |
| y2 |
| 4 |
(2)
| OS |
| OA |
| OB |
| OS |
| AB |
∴
| OA |
| OB |
|
|
∴
| OA |
| OB |
| 16 |
| 9 |
| OA |
| OB |
设l的方程为y=k(x-2),A(x1,y1),B(x2,y2)由
|
∴x1+x2=
| 36k2 |
| 9k2+4 |
| 36(k2-1) |
| 9k2+4 |
y1y2=[k(x1-2)][k(x2-2)]=k2[x1x2-2(x1+x2)+4]=-
| 20k2 |
| 9k2+4 |
把①、②代入x1x2+y1y2=0得k=±
| 3 |
| 2 |
∴存在直线l:3x-2y-6=0或3x+2y-6=0使得四边形OASB的对角线相等
点评:本题考查了消参法求轨迹方程,以及存在性问题的求法,做题时要积极思考,找到解决方法.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 ,点P是线段MN上一点,且
,点P是线段MN上一点,且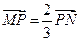 ,点P随线段MN的运动而变化.
,点P随线段MN的运动而变化.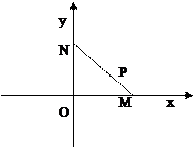
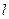 ,与曲线C交于A.B两点,O是坐标原点,设
,与曲线C交于A.B两点,O是坐标原点,设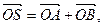 是否存在这样的直线
是否存在这样的直线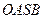 的对角线相等(即
的对角线相等(即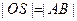 )?若存在,求出直线
)?若存在,求出直线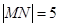 ,点P是线段MN上一点,且
,点P是线段MN上一点,且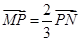 ,点P随线段MN的运动而变化.
,点P随线段MN的运动而变化.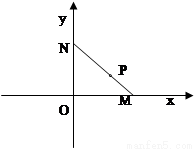
 ,与曲线C交于A.B两点,O是坐标原点,设
,与曲线C交于A.B两点,O是坐标原点,设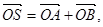 是否存在这样的直线
是否存在这样的直线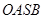 的对角线相等(即
的对角线相等(即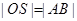 )?若存在,求出直线
)?若存在,求出直线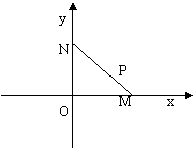 (2)过点(2,0)作直线
(2)过点(2,0)作直线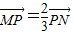 ,点P随线段MN的运动而变化.
,点P随线段MN的运动而变化.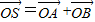 ,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.