题目内容
10.设函数f(x)=|x2-a|-ax-1(a∈R).(I)若函数y=f(x)在R上恰有四个不同的零点,求a的取值范围;
(Ⅱ)若函数y=f(x)在[1,2]上的最小值为g(a),求g(a)的表达式.
分析 (I)若函数y=f(x)在R上恰有四个不同的零点,讨论a的范围,结合一元二次函数的图象和性质即可求a的取值范围;
(Ⅱ)根据一元二次函数的单调性和对称性的关系,进行求解即可.
解答 解:(I)若函数y=f(x)在R上恰有四个不同的零点,
则等价为f(x)=|x2-a|-ax-1=0,即|x2-a|=ax+1有四个不同的解,
若a≤0,则方程x2-a=ax+1至多有两个根,不满足条件
若a>0,则y=x2-a与y=ax+1两个图象有四个不同的交点,
①当y=ax+1与y=-x2+a相切时,得a=-2±2$\sqrt{2}$,(负值舍掉),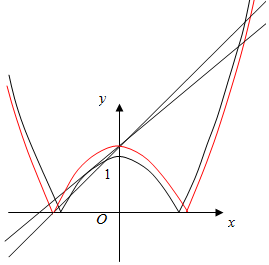
②当y=ax+1过点(-$\sqrt{a}$,0)时,得a=1,∴2$\sqrt{2}$-2<a<1,
即a的取值范围是(2$\sqrt{2}$-2,1)
(Ⅱ)①当a≤1时,f(x)=x2-ax-a-1=(x-$\frac{a}{2}$)2-$\frac{{a}^{2}}{4}$-a-1,
则f(x)在[1,2]上单调递增,则f(x)min=f(1)=-2a.
②当1<a<4时,f(x)=$\left\{\begin{array}{l}{-(x+\frac{a}{2})^{2}+\frac{{a}^{2}}{4}+a-1,}&{1≤x≤\sqrt{a}}\\{(x-\frac{a}{2})^{2}-\frac{{a}^{2}}{4}-a-a,}&{\sqrt{a}<x≤2}\end{array}\right.$,
易知f(x)在[1,$\sqrt{a}$]上单调递减,在($\sqrt{a}$,2]上单调递
则f(x)min=f($\sqrt{a}$)=-a$\sqrt{a}$-1,
③当a≥4时,f(x)=-(x+$\frac{a}{2}$)2+$\frac{{a}^{2}}{4}$+a-1,
则f(x)在[1,2]上单调递减,
则f(x)min=f(2)=-a-5,
综上g(a)=$\left\{\begin{array}{l}{-2a,}&{a≤1}\\{-a\sqrt{a}-1,}&{1<a<4}\\{-a-5,}&{a≥4}\end{array}\right.$.
点评 本题主要考查分段函数的应用,根据一元二次函数图象和性质,利用分类讨论的数学思想是解决本题的关键.综合性较强,难度较大.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案| A. | 5 | B. | 7 | C. | 10 | D. | 12 |
| A. | $\frac{1}{6}+\frac{π}{8}$ | B. | $\frac{1}{3}+\frac{π}{4}$ | C. | $\frac{1}{6}+\frac{π}{4}$ | D. | $\frac{1}{3}+\frac{π}{8}$ |
| A. | 1 | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | 2 |
| A. | 48 | B. | 36 | C. | 30 | D. | 24 |