题目内容
已知函数![]() 的图象在与x轴交点处的切线方程是
的图象在与x轴交点处的切线方程是![]() 。
。
(1)求函数![]() 的解析式;
的解析式;
(2)设函数![]() ,若
,若![]() 的极值存在,求实数
的极值存在,求实数![]() 的取值范围以及函数
的取值范围以及函数![]() 取得极值时对应的自变量
取得极值时对应的自变量![]() 的值.
的值.
(I)由已知,切点为(2,0),故有![]() ,即
,即![]() ……①
……①
又![]() ,由已知
,由已知![]() 得
得![]() ……②
……②
联立①②,解得![]() .
.
所以函数的解析式为![]()
(II)因为![]()
令![]()
当函数有极值时,则![]() ,方程
,方程![]() 有实数解,
有实数解, ![]()
![]()
由![]() ,得
,得![]() .
.
①当![]() 时,
时,![]() 有实数
有实数![]() ,在
,在![]() 左右两侧均有
左右两侧均有![]() ,故函数
,故函数![]() 无极值
无极值
②当![]() 时,
时,![]() 有两个实数根
有两个实数根
![]()
![]() 情况如下表:
情况如下表:
|
|
|
|
|
|
|
|
| + | 0 | - | 0 | + |
|
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以在![]() 时,函数
时,函数![]() 有极值;
有极值;
当![]() 时,
时,![]() 有极大值;
有极大值;
当![]() 时,
时,![]() 有极小值;
有极小值;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 对一切实数x都成立;
对一切实数x都成立; 的图象在点
的图象在点 处的切线恰好与直线
处的切线恰好与直线 平行,且
平行,且 在
在 上单调递减.
上单调递减. 的图象在
的图象在 处的切线与
处的切线与 轴平行.
轴平行. 与
与 的关系式及f(x)的极大值;
的关系式及f(x)的极大值;  在区间
在区间 上有最大值为
上有最大值为 ,试求
,试求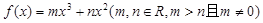 的图象在
的图象在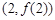 处的切线与
处的切线与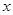 轴平行.
轴平行.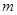 与
与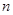 的关系式及f(x)的极大值;
的关系式及f(x)的极大值; 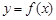 在区间
在区间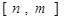 上有最大值为
上有最大值为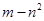 ,试求
,试求