题目内容

对于函数f（x），如果存在锐角θ使得f（x）的图象绕坐标原点逆时针旋转角θ，所得曲线仍是一函数，则称函数f（x）具备角θ的旋转性，下列函数具有角
π
4
的旋转性的是（　　）
分析：若若函数f（x）逆时针旋转角
π
4
后所得曲线仍是一函数，根据函数的定义中的“唯一性”可得函数f（x）的图象与任一斜率为1的直线y=x+b均不能有两个以上的交点，逐一分析四个答案中的函数是否满足这一性质，可得答案．
解答：解：若函数f（x）逆时针旋转角
π
4
后所得曲线仍是一函数，
则函数f（x）的图象与任一斜率为1的直线y=x+b均不能有两个以上的交点
A中函数y=
x
与直线y=x有两个交点，不满足要求；
B中函数y=lnx与直线y=x-1有两个交点，不满足要求；
C中函数y=(
1
2
)x与直线y=x+b均有且只有一个交点，满足要求；
D中函数y=x2与直线y=x有两个交点，不满足要求；
故选C
点评：本题考查的知识点是函数的定义，其中根据函数的定义分析出函数f（x）的图象与任一斜率为1的直线y=x+b均不能有两个以上的交点，是解答本题的关键．
练习册系列答案
相关题目
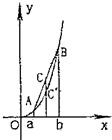精英家教网如图，对于函数f（x）=x3（x＞0）上任意两点A（a，a3），B（b，b3）线段AB在弧线段AB的上方，
AC
=
CB
，则由图中点C在C’上方可得不等式
a3+b3
2
＞(
a+b
2
)3，请分析函数y=lgx（x＞0）的图象，类比上述不等式可以得到的不等式是
 
．
给出下列四个判断：
①定义在R上的奇函数f（x），当x＞0时f（x）=x2+2，则函数f（x）的值域为{y|y≥2或y≤-2}；
②若不等式x3+x2+a＜0对一切x∈[0，2]恒成立，则实数a的取值范围是{a|a＜-12}；
③当f（x）=log3x时，对于函数f（x）定义域中任意的x1，x2（x1≠x2）都有f(
x1+x2
2
)＜
f(x1)+f(x2)
2
；
④设g（x）表示不超过t＞0的最大整数，如：[2]=2，[1.25]=1，对于给定的n∈N+，定义
C
x
n
=
n(n-1)…(n-[x]+1)
x(x-1)…(x-[x]+1)
，x∈[1，+∞），则当x∈[
3
2
，2）时函数
C
x
8
的值域是(4，
16
3
]；
上述判断中正确的结论的序号是
②④
②④
．
定义Mxn=x（x+1）（x+2）…（x+n-1）（x∈R，n∈N*），如M-44=（-4）×（-3）×（×2）×（-1）=24．对于函数f（x）=Mx-13，给出下列四个命题：
①f （x）的最大值为
2
3
9
；②f （x）为奇函数；③f（x）的图象不具备对称性；④f （x）在(-
3
3
，
3
3
)上是减函数，
真命题是
②④
②④
（填命题序号）．
如图，对于函数f（x）=x2（x＞0）的图象上不同两点A（a，a2）、B（b，b2），直线段AB
必在弧线段AB的上方，设点C分
AB
的比为λ（λ＞0），则由图象中点C在点C'上方可得不等式
a2+λb2
1+λ
＞(
a+λb
1+λ
)2．请分析函数y=lnx（x＞0）的图象，类比上述不等式，可以得到的不等式是
lna+λlnb
1+λ
＜ln
a+λb
1+λ
lna+λlnb
1+λ
＜ln
a+λb
1+λ
．
下列4个命题：
①已知函数y=2sin（x+?）（0＜?＜π）的图象如图所示，则φ=
π
6
或
5
6
π；
②在△ABC中，∠A＞∠B是sinA＞sinB的充要条件；
③定义域为R的奇函数f（x）满足f（1+x）=-f（x），则f（x）的图象关于点(
1
2
，0)对称；
④对于函数f（x）=x2+mx+n，若f（a）＞0，f（b）＞0，则f（x）在（a，b）内至多有一个零点；其中正确命题序号
②
②
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网