题目内容
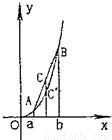
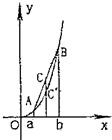 如图,对于函数f(x)=x3(x>0)上任意两点A(a,a3),B(b,b3)线段AB在弧线段AB的上方,
如图,对于函数f(x)=x3(x>0)上任意两点A(a,a3),B(b,b3)线段AB在弧线段AB的上方,| AC |
| CB |
| a3+b3 |
| 2 |
| a+b |
| 2 |
分析:根据函数f(x)=x3(x>0)的图象可知,此函数的图象是向外凹的,即可得到不等式
>(
)3,再根据对数函数的图象的特征,即可类比得到相应的不等式.
| a3+b3 |
| 2 |
| a+b |
| 2 |
解答:解:∵函数f(x)=x3(x>0)上任意两点A(a,a3),B(b,b3)线段AB在弧线段AB的上方,
=
,则由图中点C在C’上方可得不等式
>(
)3,据此我们从图象可以看出:
函数f(x)=x3(x>0)的图象是向外凹的,
类比对数函数可知,对数函数的图象是向外凸的,
故可知
<lg
,
故答案为
<lg
.
| AC |
| CB |
| a3+b3 |
| 2 |
| a+b |
| 2 |
函数f(x)=x3(x>0)的图象是向外凹的,
类比对数函数可知,对数函数的图象是向外凸的,
故可知
| lga+lgb |
| 2 |
| a+b |
| 2 |
故答案为
| lga+lgb |
| 2 |
| a+b |
| 2 |
点评:本题主要考查类比推理的知识点,解答本题的关键是熟练掌握对数函数图象的凸凹性,本题比较简单.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,对于函数f(x)=x2(x>0)的图象上不同两点A(a,a2)、B(b,b2),直线段AB
如图,对于函数f(x)=x2(x>0)的图象上不同两点A(a,a2)、B(b,b2),直线段AB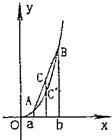
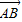 的比为λ(λ>0),则由图象中点C在点C'上方可得不等式
的比为λ(λ>0),则由图象中点C在点C'上方可得不等式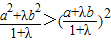 .请分析函数y=lnx(x>0)的图象,类比上述不等式,可以得到的不等式是 .
.请分析函数y=lnx(x>0)的图象,类比上述不等式,可以得到的不等式是 .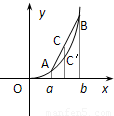
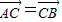 ,则由图中点C在C’上方可得不等式
,则由图中点C在C’上方可得不等式 >
>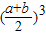 ,请分析函数y=lgx(x>0)的图象,类比上述不等式可以得到的不等式是 .
,请分析函数y=lgx(x>0)的图象,类比上述不等式可以得到的不等式是 .