题目内容
定义Mxn=x(x+1)(x+2)…(x+n-1)(x∈R,n∈N*),如M-44=(-4)×(-3)×(×2)×(-1)=24.对于函数f(x)=Mx-13,给出下列四个命题:
①f (x)的最大值为
;②f (x)为奇函数;③f(x)的图象不具备对称性;④f (x)在(-
,
)上是减函数,
真命题是
①f (x)的最大值为
2
| ||
| 9 |
| ||
| 3 |
| ||
| 3 |
真命题是
②④
②④
(填命题序号).分析:由题中条件可得,f(x)=Mx-13=(x-1)(x)(x+1)=x(x2-1)=x3-x,对函数求导可得,f′(x)=3x2-1,
①通过研究函数的单调区间求解函数的极值及最值进行判断;②利用奇函数的定义验证f(-x)=-f(x)是否成立;③结合②的讨论可进行判断即可④由①的讨论可知
①通过研究函数的单调区间求解函数的极值及最值进行判断;②利用奇函数的定义验证f(-x)=-f(x)是否成立;③结合②的讨论可进行判断即可④由①的讨论可知
解答:解:由题意可得,f(x)=Mx-13=(x-1)(x)(x+1)=x(x2-1)=x3-x
①:f′(x)=3x2-1,
由f′(x)>0可得x>
或x<-
;由f′(x)<0可得-
<x<
所以可得函数在(-∞,-
),(
,+∞)单调递增,在(-
,+
)单调递减
故可得函数在x=-
处取得极大值
,而没有最大值①错误
②:f(-x)=(-x)3+x=-x3+x=-f(x),故函数为奇函数,②正确
③:由②可得函数的图象关于原点对称③错误
④:由①的讨论可知④正确
故答案为:②④
①:f′(x)=3x2-1,
由f′(x)>0可得x>
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
所以可得函数在(-∞,-
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
故可得函数在x=-
| ||
| 3 |
2
| ||
| 9 |
②:f(-x)=(-x)3+x=-x3+x=-f(x),故函数为奇函数,②正确
③:由②可得函数的图象关于原点对称③错误
④:由①的讨论可知④正确
故答案为:②④
点评:本题以新定义为载体,综合考查了函数的性质,解答本题的关键是要根据题目中的定义求解出函数的解析式,进而结合导数的知识求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
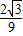 ;②f (x)为奇函数;③f(x)的图象不具备对称性;④f (x)在
;②f (x)为奇函数;③f(x)的图象不具备对称性;④f (x)在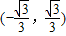 上是减函数,
上是减函数,