题目内容
16.中心在原点,焦点在x轴上的一椭圆与一双曲线有共同的焦点F1、F2,且F1F2=2$\sqrt{13}$,椭圆的长半轴长与双曲线实际轴长之差为4,离心率之比为3:7.(1)求这两曲线方程;
(2)若P为这两曲线的一个交点,求△F1PF2的面积.
分析 (1)根据半焦距c=$\sqrt{13}$,设椭圆长半轴为a,由离心率之比求出a,进而求出椭圆短半轴的长及双曲线的虚半轴的长,写出椭圆和双曲线的标准方程;
(2)由椭圆、双曲线的定义求出PF1与PF2的长,在三角形F1PF2中,利用余弦定理求出 cos∠F1PF2 的值,进一步求得sin∠F1PF2 的值,代入面积公式得答案.
解答 解:(1)由题意知,半焦距c=$\sqrt{13}$,设椭圆长半轴为a,则双曲线实半轴a-4,
离心率之比为$\frac{3}{7}$=$\frac{\frac{\sqrt{13}}{a}}{\frac{\sqrt{13}}{a-4}}$,解得a=7,
∴椭圆的短半轴长等于$\sqrt{49-13}=6$,
双曲线虚半轴的长为$\sqrt{13-9}=2$,
∴椭圆和双曲线的方程分别为:$\frac{{x}^{2}}{49}+\frac{{y}^{2}}{36}=1$和$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}=1$;
(2)由椭圆的定义得:PF1 +PF2=2a=14,
由双曲线的定义得:PF1-PF2=6,
∴PF1=10,PF2=4,
又F1F2=2$\sqrt{13}$,在三角形F1PF2中,利用余弦定理得:$(2\sqrt{13})^{2}$=100+16-80cos∠F1PF2,
∴cos∠F1PF2=$\frac{4}{5}$,则sin$∠{F}_{1}P{F}_{2}=\frac{3}{5}$.
∴${S}_{△{F}_{1}P{F}_{2}}$=$\frac{1}{2}P{F}_{1}•P{F}_{2}•sin∠{F}_{1}P{F}_{2}$=$\frac{1}{2}×10×4×\frac{3}{5}=12$.
点评 本题主要考查椭圆、双曲线的标准方程和几何性质、平面向量数量积的运算,考查计算能力,是中档题.

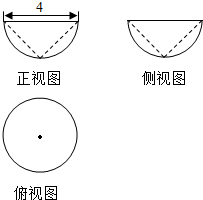 如图为一个半球挖去一个圆锥后的几何体的三视图,则剩余部分与挖去部分的体积之比为( )
如图为一个半球挖去一个圆锥后的几何体的三视图,则剩余部分与挖去部分的体积之比为( )| A. | 3:1 | B. | 2:1 | C. | 1:1 | D. | 1:2 |
| A. | $\frac{17\sqrt{17}}{6}π$ | B. | 17π | C. | $\frac{17π}{2}$ | D. | $\frac{17π}{4}$ |
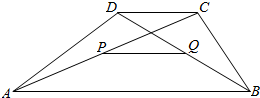 设P,Q分别是梯形ABCD的对角线AC与BD的中点
设P,Q分别是梯形ABCD的对角线AC与BD的中点 ,圆心角
,圆心角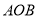 的大小等于
的大小等于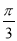 ,半径为
,半径为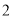 百米,在半径
百米,在半径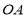 上取一点
上取一点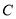 ,过点
,过点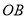 的直线交弧
的直线交弧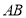 于点
于点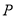 .设
.设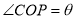 .
.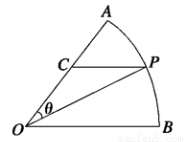
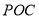 面积
面积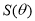 的函数表达式.
的函数表达式.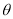 的值.
的值.