Question

【题目】如图，抛物线的焦点为F，准线为，交x轴于点A，并截圆所得弦长为，M为平面内动点，△MAF周长为6．

（1）求抛物线方程以及点M的轨迹的方程；

（2）“过轨迹的一个焦点作与轴不垂直的任意直线”交轨迹于两点，线段的垂直平分线交轴于点，则为定值，且定值是”.命题中涉及了这么几个要素：给定的圆锥曲线，过该圆锥曲线焦点的弦，的垂直平分线与焦点所在的对称轴的焦点，的长度与、两点间距离的比值.试类比上述命题，写出一个关于抛物线的类似的正确命题，并加以证明.

（3）试推广（2）中的命题，写出关于抛物线的一般性命题（不必证明）.

Answer 1

【答案】（1），；（2）过抛物线的焦点作与轴不垂直的任意直线，交抛物线于两点，线段的垂直平分线交轴于点，则为定值，且定值为，证明见解析；（3）过抛物线的焦点作与对称轴不垂直的任意直线，交抛物线于两点，线段的垂直平分线交对称轴于点，则为定值，且定值为．

【解析】

（1）根据弦长公式可求出弦心距，即得准线的方程和点的坐标，从而可求出抛物线方程，再根据△MAF周长为6，设出点，根据椭圆的定义即可求出点M的轨迹的方程；

（2）根据题意类比即可写出；

（3）利用（2）中原理，即可写出．

（1）设圆心到直线的距离为，∴，解得．

所以准线：，点，点，即有，∴，即抛物线．

因为，所以，即点的轨迹是以点为焦点，长轴长为，焦距为的椭圆，∴，解得，即有．

故点M的轨迹的方程为．

（2）关于抛物线的类似的正确命题为：过抛物线的焦点作与轴不垂直的任意直线，交抛物线于两点，线段的垂直平分线交轴于点，则为定值，且定值为．证明如下：

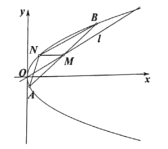
如图所示：

设直线：

由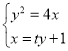得，，设，

所以，，

即的中点坐标为，

的垂直平分线的方程为：，令，解得，

∴．

又因为，所以．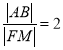

（3）过抛物线的焦点作与对称轴不垂直的任意直线，交抛物线于两点，线段的垂直平分线交对称轴于点，则为定值，且定值为．