题目内容
【题目】已知
，抛物线C：
的焦点到直线l：
的距离为
.
（1）求m的值.
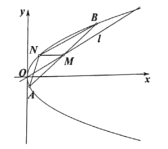
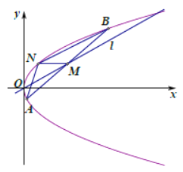
（2）如图，已知抛物线C的动弦
的中点M在直线l上，过点M且平行于x轴的直线与抛物线C相交于点N，求
面积的最大值.
【答案】（1）
；（2）16.
【解析】
(1)列出抛物线的焦点到直线l的距离公式即可求解；
(2)设出直线
的方程与抛物线联立，即可得出点M, N坐标，求出点N到直线的距离及弦的长度，即可表示出
的面积，结合二次函数的性质即可求解.
（1）抛物线C的焦点
.
由题设得，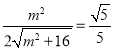
，解得
，
因为
，所以．
（2）设直线方程为
，代入抛物线方程
得，
，
则
，①
设
，
，
，
则
，所以
，
，
因为点M在l上，则有
，即
，②
将②代入①得
，解得
，
易得N的坐标为
，
则点N到直线的距离
，
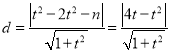， 所以
，
当
时取到等号，所以
面积的最大值为16．
练习册系列答案
阅读快车系列答案
相关题目
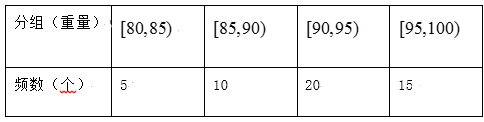
【题目】随着社会经济高速发展，人民的生活水平越来越高，部分学校安装了中央空调，某校数学建模队调查了某品牌中央空调，得到该设备使用年限x（单位：年）和维修总费用y（单位：万元）的统计表如下：（每年年底维修保养）
使用年限x（单位：年） | 2 | 3 | 4 | 5 | 6 |
维修总费用y（单位：万元） | 1 |
| 3 | 4 |
|
由上表可得线性回归方程
，则根据此模型预报该品牌中央空调第8年年底的维修费用约为（ ）
A.
万元B.
万元C.
万元D.
万元
