Question

12．已知函数f（x）=kx²+（k-3）x+1的图象与x轴在原点的右侧有交点，试确定实数k的取值范围．

Answer 1

分析 根据题意，二次函数的图象与x轴在原点的右侧有公共点，有两种情况，一是只有一个在右侧，二是两个都在右侧，分类讨论即可．

解答 解：（1）当k=0时，f（x）=-3x+1，直线与x轴的交点为（$\frac{1}{3}$，0），在原点右侧，符合题意；
（2）当k≠0时，∵f（0）=1，∴抛物线过点（0，1）；
若k＜0时，f（x）的开口向下，对称轴x=-$\frac{k-3}{2k}$＜0，如图所示；

∴二次函数的图象与x轴的交点必然是一个在原点右侧，一个在原点左侧，满足题意；
若k＞0，f（x）的开口向上，如图所示，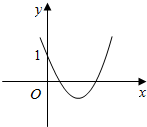

要使函数的零点在原点右侧，当且仅当△=（k-3）²-4k≥0，
且对称轴x=-$\frac{k-3}{2k}$＞0即可，如图所示，解得：1≤k＜3；
综上，k的取值范围是[1，3）∪（-∞，0]．

点评 本题考查了一元二次方程根的分布与系数的关系，也考查了分类讨论思想的应用问题，是中档题．