题目内容
【题目】已知关于
的一元二次函数
（1）若
分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次正面朝上出现的点数，求满足函数
在区间[
上是增函数的概率；
（2）设点
是区域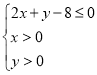
内的随机点，求函数在区间
上是增函数的概率.
【答案】(1)
;(2) 
【解析】
（1）由题意函数
在区间[
上是增函数，可得
，
，可得可得先后抛掷两次骰子的基本事件数为36个，求出所求事件包含基本事件，可得其概率；
（2）由（1）可得，，可得实验的全部结果所构成的区域与所求事件所构成的区域，由几何概型可得答案.
解：可得函数
的对称轴为：
，
要使函数在区间[上是增函数，当且仅当，
，，
由题意可得先后抛掷两次骰子的基本事件数为36个，
所求事件包含基本事件：
，
所求事件包含的事件为为9个，
可得所求事件的概率为：
；
（2）由（1）得，要使函数在区间[上是增函数，当且仅当，，，
由题意可得实验的全部结果所构成的区域是：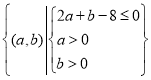
，
构成所求事件的区域为三角形部分，
由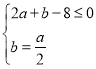
得交点坐标
，
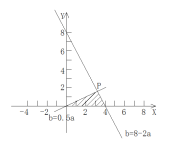
可得所求事件概率为：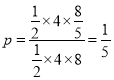
练习册系列答案
世纪百通期末金卷系列答案
相关题目
