题目内容
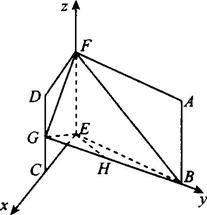
1.如图所示,设AB、CD是夹在两个平行平面α、β之间的异面直线段,M、N分别为AB、CD的中点,求证:MN∥α.

2.在本题中,若AB、AE是夹在两个平行平面α、β之间的两条相交线段,且M、N分别为AB、AE的中点,如何证明MN∥α?
3.在本题中,若AB、CD是夹在两个平行平面α、β之间的两条平行线段,M、N分别为AB、CD的中点,如何证明MN∥α?
答案:
解析:
提示:
解析:
|
1.
2. 3. 思路分析:要证明MN∥α,由于AB、CD为异面直线,所以要在α内找一条直线,证明它与MN平行较为困难,因此可转化为证明过MN的一个平面与平面α平行. |
提示:
|
本题的证法较多,解题关键是如何处理好条件:AB、CD是两条异面线段.证法一实质上是把CD在两平行平面间沿着同一方向移到AE位置,AB和AE可确定一平面,借助于平面几何来处理问题;证法二是借助于空间四边形的对角线AD,把AB和CD分别放在两相交平面内来研究.本题还可以连结CM,延长交α于点R,证明MN∥RD即可. |

练习册系列答案
相关题目




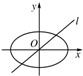 如图所示,设椭圆
如图所示,设椭圆
 如图所示,设铁路AB=50,B、C之间距离为10,现将货物从A运往C,已知单位距离铁路费用为2,公路费用为4,问在AB上何处修筑公路至C,可使运费由A到C最省?
如图所示,设铁路AB=50,B、C之间距离为10,现将货物从A运往C,已知单位距离铁路费用为2,公路费用为4,问在AB上何处修筑公路至C,可使运费由A到C最省?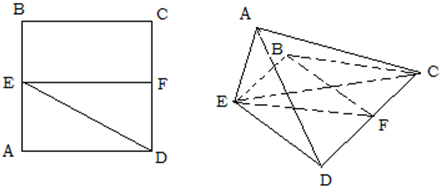 已知正方形ABCD,E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示.设二面角A-DE-C的大小为90°.
已知正方形ABCD,E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示.设二面角A-DE-C的大小为90°.