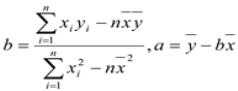题目内容
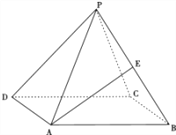
【题目】如图,四棱锥![]() 的底面
的底面![]() 为正方形,
为正方形,![]() ⊥底面
⊥底面![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,![]() .
.
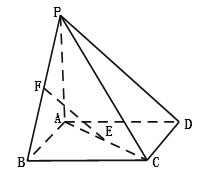
(Ⅰ)求证![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成的角;
所成的角;
(Ⅲ)求四棱锥![]() 的外接球的体积.
的外接球的体积.
【答案】(Ⅰ)见解析;(Ⅱ)45°;(Ⅲ)![]() .
.
【解析】试题分析:(Ⅰ)欲证![]() ∥平面
∥平面![]() ;连
;连![]() ,根据中位线可以知道
,根据中位线可以知道![]() ,而
,而![]() 不在平面
不在平面![]() 内,满足定理所需条件;
内,满足定理所需条件;
(Ⅱ)关键是证明![]() 平面
平面![]() ,找到
,找到![]() 是直线
是直线![]() 与平面
与平面![]() 所成的角;
所成的角;
(Ⅲ)利用补成正方体的思想,求外接球的半径.
试题解析:(Ⅰ)如图,连结![]() ,则
,则![]() 是
是![]() 的中点,又
的中点,又![]() 是
是![]() 的中点,
的中点,
∴![]() .又∵
.又∵![]() 平面
平面![]() ,
,![]() 面
面![]()
∴![]() 平面
平面![]() .
.
(Ⅱ)取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
在正方形![]() 中,
中,![]() 是
是![]() 的中点,有
的中点,有![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() 是直线
是直线![]() 在平面
在平面![]() 的射影,∴
的射影,∴![]() 是直线
是直线![]() 与平面
与平面![]() 所成的角,
所成的角,
在直角三角形![]() 中,
中,![]() ,所以
,所以![]() .
.
∴直线![]() 与平面
与平面![]() 所成的角为45°.
所成的角为45°.
(Ⅲ)设四棱锥![]() 的外接球半径为
的外接球半径为![]() ,
,![]() ,则
,则
![]() ,即
,即![]() .
.
所以外接球的体积为![]() .
.

练习册系列答案
相关题目