题目内容
【题目】已知x0,x0+![]() 是函数f(x)=cos2(wx﹣
是函数f(x)=cos2(wx﹣![]() )﹣sin2wx(ω>0)的两个相邻的零点
)﹣sin2wx(ω>0)的两个相邻的零点
(1)求![]() 的值;
的值;
(2)若对任意![]() ,都有f(x)﹣m≤0,求实数m的取值范围.
,都有f(x)﹣m≤0,求实数m的取值范围.
(3)若关于![]() 的方程
的方程![]() 在
在![]() 上有两个不同的解,求实数
上有两个不同的解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(1)利用三角恒等变形,对原函数进行化简变形,可得![]() ,由两相邻零点可得函数最小正周期,再利用最小正周期与
,由两相邻零点可得函数最小正周期,再利用最小正周期与![]() 的关系可得函数表达式,将
的关系可得函数表达式,将![]() 代入可得其值;(2)实数
代入可得其值;(2)实数![]() 的取值范围可转化为求函数
的取值范围可转化为求函数![]() 在
在![]() 的最大值问题,利用三角函数的性质可得结果;(3)类比第二小题,利用分离变量求出
的最大值问题,利用三角函数的性质可得结果;(3)类比第二小题,利用分离变量求出![]() 的取值范围,结合图象可知与
的取值范围,结合图象可知与![]() 有两交点时
有两交点时![]() 的范围.
的范围.
试题解析:(1)f(x)=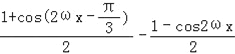 =
=![]()
=![]() =
=![]()
=![]() (
(![]() )=
)=![]() .
.
由题意可知,f(x)的最小正周期T=π,
∴![]() , 又∵ω>0, ∴ω=1,
, 又∵ω>0, ∴ω=1,
∴f(x)=![]() .
.
∴![]() =
=![]() .
.
(2)由f(x)﹣m≤0得,f(x)≤m, ∴m≥f(x)max,
∵﹣![]() , ∴
, ∴![]() , ∴
, ∴![]() ,
,
∴﹣![]() ≤
≤![]() , 即f(x)max=
, 即f(x)max=![]() ,
,
∴![]() 所以
所以![]()
(3)原方程可化为![]()
即![]()
![]()
画出![]()
![]() 的草图
的草图
x=0时,y=2sin![]() =
=![]() ,
,
y的最大值为2,
∴要使方程在x∈[0, ![]() ]上有两个不同的解,
]上有两个不同的解,
即![]() ≤m+1<2, 即
≤m+1<2, 即![]() ﹣1≤m<1. 所以
﹣1≤m<1. 所以![]()

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目