题目内容
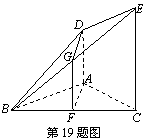
如图，AD
平面ABC，AD∥CE，AC=AD=AB=1，∠BAC=90°，凸多面体ABCED的体积为
，F为BC的中点.
（Ⅰ）求证：AF∥平面BDE；
（Ⅱ）求证：平面BDE平面BCE.
（Ⅰ）证明：∵AD⊥平面ABC，AC
面ABC，AB面ABC，
∴AD⊥AC，AD⊥AB，
∵AD∥CE，∴CE⊥AC
∴四边形ACED为直角梯形.……………（1分）
又∵∠BAC=90°，∴AB⊥AC，∴AB⊥面ACED.
………………（2分）
∴凸多面体ABCED的体积
求得CE=2.……………………………………………………（3分）
取BE的中点G，连结GF，GD，
则GF∥EC，GF
CE=1，
∴GF∥AD，GF=AD，四边形ADGF为平行四边形，
∴AF∥DG.………………………………………………………（5分）
又∵GD面BDE，AF
面BDE，
∴AF∥平面BDE.………………………………………………（7分）
（Ⅱ）证明：∵AB=AC，F为BC的中点，
∴AF⊥BC.………………………………………………………（8分）
由（Ⅰ）知AD⊥平面ABC，AD∥GF，∴GF⊥面ABC.
∵AF面ABC，∴AF⊥GF. ……………………………………（9分）
又BC
GF=F，∴AF⊥面BCE.…………………………………（10分）
又∵DG∥AF，∴DG⊥面BCE.……………………………（11分）
∵DG面BDE，∴面BDE⊥面BCE
仁爱英语同步练习册系列答案
学习实践园地系列答案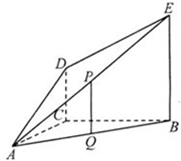
如图，DC⊥平面ABC，EB∥DC，AC=BC=EB=2DC=2，∠ACB=120°，P，Q分别为AE，AB的中点．
（2013•临沂二模）如图，AD⊥平面ABC，AD∥CE，AC=AD=AB=1，∠BAC=90°，凸多面体ABCED的体积为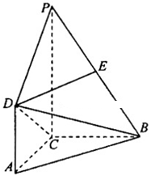
（2013•和平区一模）如图，PC⊥平面ABC，DA∥PC，∠ACB=90°，E为PB的中点，AC=AD=BC=1，PC=2．
，F为BC的中点．