Question

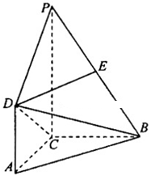（2013•和平区一模）如图，PC⊥平面ABC，DA∥PC，∠ACB=90°，E为PB的中点，AC=AD=BC=1，PC=2．
（I）求证：DE∥平面ABC：
（II）求证：PD⊥平面BCD；
（III）设Q为PB上一点，

PQ

=λ

PB

，试确定λ的值使得二面角Q-CD-B为45°．

Answer 1

分析：（I）建立如图所示的空间直角坐标系，可知

PC

=(0，0，2)为平面ABC的一个法向量，利用

DE

•

PC

=0?

DE

⊥

PC

，DE?平面ABC，?DE∥平面ABC即可证明．
（II）利用

PD

•

BC

=0?PD⊥BC，

PD

•

CD

=0?PD⊥CD．及BC∩DC=C，即可证明PD⊥平面BCD．
（III）由（II）可知：

PD

=（1，0，-1）为平面BCD的法向量，由

PB

=(0，1，-2)，

PQ

=λ

PB

=(0，λ，-2λ)，λ∈（0，1），可得Q（0，λ，-2λ+2）．再求出平面QCD的一个法向量，利用两个法向量的夹角即可得出二面角的余弦值．

解答：（I）证明：建立如图所示的空间直角坐标系，则B（0，1，0），D（1，0，1），P（0，0，2），E(0，

1

2

，1)，

DE

=(-1，

1

2

，0)．
可知

PC

=(0，0，2)为平面ABC的一个法向量，
∵

DE

•

PC

=0，∴

DE

⊥

PC

．
∵DE?平面ABC，∴DE∥平面ABC．
（II）证明：∵

PD

=(1，0，-1)，

BC

=（0，1，0），

CD

=（1，0，1）．
∴

PD

•

BC

=0，

PD

•

CD

=0．
∴PD⊥BC，PD⊥CD．∵BC∩DC=C，
∴PD⊥平面BCD．
（III）解：由（II）可知：

PD

=（1，0，-1）为平面BCD的法向量，
∵

PB

=(0，1，-2)，

PQ

=λ

PB

=(0，λ，-2λ)，λ∈（0，1）．
∴Q（0，λ，-2λ+2）．
设平面QCD的法向量为

n

=(x，y，z)，由

n • CD =0 n • CQ =0

，得

x+z=0 λy+(-2λ+2)z=0

，
令z=1，则x=-1，y=

2

λ

-2，∴

n

=(-1，

2

λ

-2，1)，λ∈（0，1）．
∴cos45°=

| n • PD |

| n | | PD |

=

2

2 × 2+( 2 λ -2)2

=

2

2

，
解得λ=2-

2

．

点评：本题综合考查了通过建立空间直角坐标系利用向量证明线面平行与垂直、利用平面的法向量求二面角的余弦值等基础知识与基本技能，考查了空间想象能力、推理能力和计算能力．