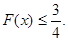题目内容
设函数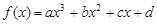 (a、b、c、d∈R)满足:对于任意的
(a、b、c、d∈R)满足:对于任意的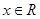 都有f(x)+f(-x)=0,且x=1时f(x)取极小值
都有f(x)+f(-x)=0,且x=1时f(x)取极小值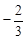 .
.
(1)f(x)的解析式;
(2)当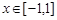 时,证明:函数图象上任意两点处的切线不可能互相垂直:
时,证明:函数图象上任意两点处的切线不可能互相垂直:
【答案】
解:(1)因为
 成立,所以
成立,所以 ,由
,由 得3a+c=0,(2分)
得3a+c=0,(2分)
由: ,得
,得 …4分
…4分
解之得: ,
, 从而,函数解析式为:
从而,函数解析式为: …6分
…6分
(2)由于, ,设:任意两数x1,
,设:任意两数x1, 是函数f(x)图像上两点的横坐标,则这两点的切线的斜率分别是:
是函数f(x)图像上两点的横坐标,则这两点的切线的斜率分别是:
 ,
,
 …(9分)
…(9分)
又因为: ,
, ,所以,
,所以, ,
, ,得:
,得: 知:
知:
故,当 是函数f(x)图像上任意两点的切线不可能垂直 …………12分
是函数f(x)图像上任意两点的切线不可能垂直 …………12分
【解析】略

练习册系列答案
相关题目
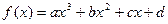 (a、b、c、d∈R)满足:
(a、b、c、d∈R)满足: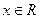 都有
都有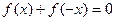 ,
,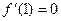 ,
,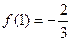
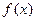 的解析式;
的解析式;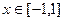 时,证明:函数图象上任意两点处的切线不可能互相垂直;
时,证明:函数图象上任意两点处的切线不可能互相垂直;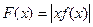 ,证明:
,证明: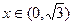 时,
时,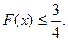
 =(x-a)(x-b)(x-c),(a,b,c是两两不等的常数),则
=(x-a)(x-b)(x-c),(a,b,c是两两不等的常数),则 +
+ +
+ 等于( )
等于( )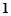 (C)
(C) (D)
(D) 
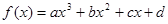 (a、b、c、d∈R)满足:
(a、b、c、d∈R)满足: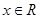 都有
都有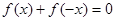 ,
,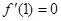 ,
,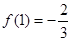
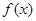 的解析式;
的解析式;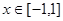 时,证明:函数图象上任意两点处的切线不可能互相垂直;
时,证明:函数图象上任意两点处的切线不可能互相垂直;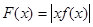 ,证明:
,证明: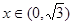 时,
时,