题目内容
若关于x的一元二次不等式ax2+bx+c<0的解集为 或
或 ,求关于x的不等式cx2-bx+a>0的解集.
,求关于x的不等式cx2-bx+a>0的解集.
【答案】分析:根据不等式ax2+bx+c<0的解为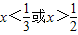 ,可得出a<0,
,可得出a<0,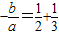 ,
, ,然后将要求的不等式两边同时除以a即可得出各项的系数,进而可解得答案.
,然后将要求的不等式两边同时除以a即可得出各项的系数,进而可解得答案.
解答:解:由题意得:a<0,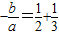 =
= ,
,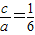 ,
,
不等式cx2+bx+a>0可化为: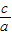 x2+
x2+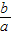 x+1<0,
x+1<0,
即 x2
x2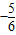 x+1>0,
x+1>0,
化简得(x-3)(x-2)>0,
解得:x>3或x<2.
∴所求不等式的解集为{x|x<2或x>3}.
点评:本题考查了一元二次不等式的知识,有一定的难度,本题的技巧性较强,关键是利用根与系数的关系得出第二个不等式的各项的系数,在解答此类题目时要注意与一元二次方程的结合.
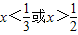 ,可得出a<0,
,可得出a<0,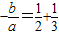 ,
, ,然后将要求的不等式两边同时除以a即可得出各项的系数,进而可解得答案.
,然后将要求的不等式两边同时除以a即可得出各项的系数,进而可解得答案.解答:解:由题意得:a<0,
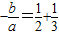 =
= ,
,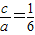 ,
,不等式cx2+bx+a>0可化为:
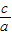 x2+
x2+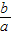 x+1<0,
x+1<0,即
 x2
x2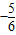 x+1>0,
x+1>0,化简得(x-3)(x-2)>0,
解得:x>3或x<2.
∴所求不等式的解集为{x|x<2或x>3}.
点评:本题考查了一元二次不等式的知识,有一定的难度,本题的技巧性较强,关键是利用根与系数的关系得出第二个不等式的各项的系数,在解答此类题目时要注意与一元二次方程的结合.

练习册系列答案
相关题目