题目内容
设函数 ,数列
,数列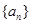 满足
满足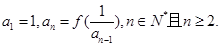
(1)求数列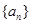 的通项公式;
的通项公式;
(2)对 ,设
,设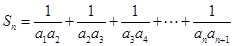 ,若
,若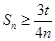 恒成立,求实数
恒成立,求实数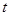 的取值范围.
的取值范围.
(1)  .(2)
.(2)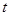 的取值范围是
的取值范围是 .
.
解析试题分析:(1)由 可得:
可得: .所以这是一个等差数列,由等差数列的通项公式即可得.(2)
.所以这是一个等差数列,由等差数列的通项公式即可得.(2) ,
, .这是典型的用裂项法求和的数列. 由
.这是典型的用裂项法求和的数列. 由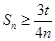 得
得 .要使得
.要使得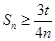 恒成立,则
恒成立,则 .用裂项法可求得
.用裂项法可求得 ,从而得
,从而得 ,令
,令 .下面求
.下面求 的最小值.将
的最小值.将 变形得
变形得 .利用函数
.利用函数 的单调性便可得
的单调性便可得 最小值,进而得
最小值,进而得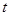 的取值范围.
的取值范围.
试题解析:(1)由 可得:
可得: .
.
所以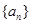 是等差数列.
是等差数列.
又因为 .
.
(2)  .
. ,
, .
. .
. 恒成立.
恒成立.
令 .
. .
.
令 ,则
,则 .
. ,易知
,易知 时,
时, 最小.
最小.
所以 ,即
,即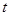 的取值范围是
的取值范围是 .
.
考点:1、等差数列;2、裂项求和;3、不等关系.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 满足
满足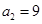 ,且
,且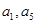 是方程
是方程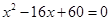 的两根。
的两根。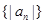 的前n项和
的前n项和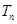 。
。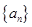 中,
中,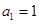 ,对任意的
,对任意的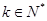 ,
,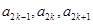 成等比数列,公比为
成等比数列,公比为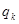 ;
;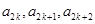 成等差数列,公差为
成等差数列,公差为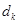 ,且
,且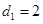 .
.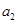 的值;
的值;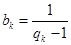 ,证明:数列
,证明:数列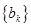 为等差数列;
为等差数列;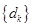 的前
的前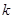 项和
项和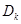 .
.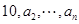 是各项均不为零的
是各项均不为零的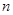 (
(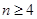 )项等差数列,且公差
)项等差数列,且公差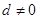 .
. ,且该数列前
,且该数列前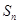 最大,求
最大,求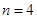 ,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求
,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求 的值;
的值;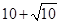 ,则数列
,则数列 中,
中,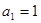 ,
,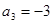 .
.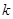 项和
项和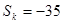 ,求
,求 的前
的前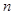 项和为
项和为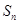 ,且
,且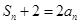 ,数列
,数列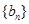 满足
满足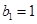 ,且
,且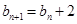 .
.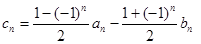 ,求数列
,求数列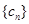 的前
的前 项和
项和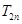 .
.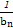 }的前n项和Tn.
}的前n项和Tn.