题目内容
18.已知函数$f(x)=3sin({2x+\frac{π}{4}})({x∈R})$(1)函数f(x)的单调区间.
(2)求函数f(x)取得最大值、最小值的自变量x的集合,并分别写出最大值、最小值是什么?
分析 (1)将内层函数看作整体,放到正弦函数的增减区间上,解不等式得函数的单调递增减区间;
(2)根据三角函数的图象和性质,令2x+$\frac{π}{4}$=$\frac{π}{2}+2kπ$和2x+$\frac{π}{4}$=-$\frac{π}{2}+2kπ$求出f(x)的最大值和最小值自变量x的集合.
解答 解:函数$f(x)=3sin({2x+\frac{π}{4}})({x∈R})$
由-$\frac{π}{2}+2kπ$≤2x+$\frac{π}{4}$≤$\frac{π}{2}+2kπ$,k∈Z.
得$kπ-\frac{3π}{8}≤x≤kπ+\frac{π}{8}$,
∴单调递增区间$[{kπ-\frac{3π}{8},kπ+\frac{π}{8}}]({k∈Z})$,
由$\frac{π}{2}+2kπ$≤2x+$\frac{π}{4}$≤$\frac{3π}{2}+2kπ$,k∈Z.
得$kπ+\frac{π}{8}≤x≤kπ+\frac{5π}{8}$,
单调递减区间$[{kπ+\frac{π}{8},kπ+\frac{5π}{8}}]({k∈Z})$.
(2)根据三角函数的图象和性质,当2x+$\frac{π}{4}$=$\frac{π}{2}+2kπ$时,即x=kπ$+\frac{π}{8}$时,y取得最大值3.
当2x+$\frac{π}{4}$=-$\frac{π}{2}+2kπ$,即x=kπ$-\frac{3π}{8}$时,y取得最大值-3
∴函数f(x)取得最大值自变量x的集合为$\left\{{x\left|{x=kπ+\frac{π}{8},k∈Z}\right.}\right\}$,y的最大值3
函数f(x)取得最小值自变量x的集合为$\left\{{x\left|{x=kπ-\frac{3π}{8},k∈Z}\right.}\right\}$,y的最大值-3.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用.属于基础题.

 名校课堂系列答案
名校课堂系列答案
| A. | 5040 | B. | 4850 | C. | 2450 | D. | 2550 |
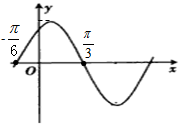 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{12}$单位得到的部分图象如图,则φ=( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{12}$单位得到的部分图象如图,则φ=( )| A. | $\frac{π}{6}$ | B. | -$\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{2}$ |
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{2}$或-2 | C. | $\frac{1}{2}$或2 | D. | -2 |

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
| A. | 0 | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |