Question

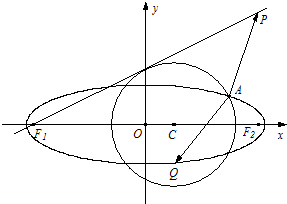已知点P（4，4），圆C：（x-m）²+y²=5（m＜3）与椭圆E：

x2

a2

+

y2

b2

=1（a＞b＞0）有一个公共点A（3，1），F₁、F₂分别是椭圆的左、右焦点，直线PF₁与圆C相切．
（Ⅰ）求m的值与椭圆E的方程；
（Ⅱ）设Q为椭圆E上的一个动点，求

AP

•

AQ

的取值范围．

Answer 1

分析：（1）先利用点A在圆上求出m，再利用直线PF₁与圆C相切求出直线PF₁与的方程以及c，再利用点A在椭圆上求出2a，即可求出椭圆E的方程；
（2）先把

AP

•

AQ

用点Q的坐标表示出来，再利用Q为椭圆E上的一个动点以及基本不等式即可求出

AP

•

AQ

的取值范围．

解答：解：（1）点A代入圆C方程，得（3-m）²+1=5．
∵m＜3，
∴m=1．
设直线PF₁的斜率为k，
则PF₁：y=k（x-4）+4，即kx-y-4k+4=0．
∵直线PF₁与圆C相切，圆C：（x-1）²+y²=5，
∴

|k-0-4k+4|

k2+1

=

5

，
解得k=

11

2

，或k=

1

2

．
当k=

11

2

时，直线PF₁与x轴的交点横坐标为

36

11

，不合题意，舍去．
当k=

1

2

时，直线PF₁与x轴的交点横坐标为-4，
∴c=4．
∴F₁（-4，0），F₂（4，0）．
故2a=AF₁+AF₂=5

2

+

2

=6

2

，a=3

2

，a²=18，b²=2．
椭圆E的方程为：

x2

18

+

y2

2

=1．
（2）

AP

=(1， 3)，设Q（x，y），

AQ

=(x-3， y-1)，

AP

•

AQ

=(x-3)+3(y-1)=x+3y-6．
∵

x2

18

+

y2

2

=1，即x²+（3y）²=18，而x²+（3y）²≥2|x|•|3y|，
∴-18≤6xy≤18．
则（x+3y）²=x²+（3y）²+6xy=18+6xy的取值范围是[0，36]．
∴x+3y的取值范围是[-6，6]
∴x+3y-6的范围只：[-12，0]．
即

AP

•

AQ

的取值范围是[-12，0]．

点评：本题是对圆与椭圆知识的综合考查．当直线与圆相切时，可以利用圆心到直线的距离等于半径求解．，也可以把直线与圆的方程联立让对应方程的判别式为0求解．