题目内容

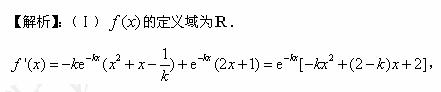 即
即 ![]() .令
.令![]() ,解得:
,解得:![]() 或
或![]() .
.
当![]() 时,
时,![]() ,故
,故![]() 的单调递增区间是
的单调递增区间是![]() .……3分
.……3分
当![]() 时,
时,![]() ,
,![]() 随
随![]() 的变化情况如下:
的变化情况如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大值 |
| 极小值 |
|
所以,函数![]() 的单调递增区间是
的单调递增区间是![]() 和
和![]() ,单调递减区间是
,单调递减区间是![]() .……5分
.……5分
当![]() 时,
时,![]() ,
,![]() 随
随![]() 的变化情况如下:
的变化情况如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大值 |
| 极小值 |
|
所以,函数![]() 的单调递增区间是
的单调递增区间是![]() 和
和![]() ,单调递减区间是
,单调递减区间是![]() .…7分
.…7分
(Ⅱ)当![]() 时,
时,![]() 的极大值等于
的极大值等于![]() . 理由如下:当
. 理由如下:当![]() 时,
时,![]() 无极大值.
无极大值.
当![]() 时,
时, ![]() 的极大值为
的极大值为![]() ,…8分
,…8分
令![]() ,即
,即![]() 解得
解得 ![]() 或
或![]() (舍)…9分 当
(舍)…9分 当![]() 时,
时,![]() 的极大
的极大
值为![]() .……10分因为
.……10分因为 ![]() ,
,![]() 所以
所以 ![]() .因为
.因为 ![]() ,所以
,所以
![]() 的极大值不可能等于
的极大值不可能等于![]() .综上所述,当
.综上所述,当![]() 时,
时,![]() 的极大值等于
的极大值等于![]() ……12分
……12分

练习册系列答案
相关题目
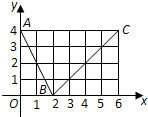 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=