Question

3．某市规定，高中学生三年在校期间参加不少于₈₀小时的社区服务才合格．教育部门在全市随机抽取200位学生参加社区服务的数据，按时间段，[75，80），[80，85），[85，90），[90，95）[95，100]，（单位：小时）进行统计，其频率分布直方图如图所示．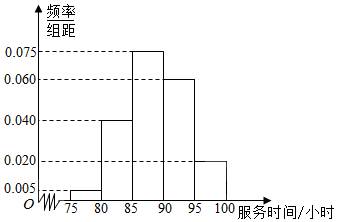

（1）求抽取的200位学生中，参加社区服务时间不少于90小时的学生人数，并估计从全市高中学生中任意选取一人，其参加社区服务时间不少于90小时的概率；
（2）从全市高中学生（人数很多）中任意选取3位学生，记ξ为3位学生中参加社区服务时间不少于90小时的人数．试求随机变量ξ的分布列和数学期望Eξ和方差Dξ．

Answer 1

分析 （1）分别求出参加社区服务时间在时间段[90，95）小时的学生人数和参加社区服务时间在时间段[95，100]小时的学生人数，由此能求出从全市高中学生中任意选取一人，其参加社区服务时间不少于90小时的概率．
（2）从全市高中生中任意选取1人，其参加社区服务时间不少于90小时的概率为$\frac{2}{5}$．由已知得，随机变量ξ的可能取值为0，1，2，3，ξ～$B（3，\frac{2}{5}）$，由此能求出随机变量ξ的分布列和数学期望Eξ和方差Dξ．

解答 解：（1）根据题意，参加社区服务时间在时间段[90，95）小时的学生人数为0.060×5×200=60（人），
参加社区服务时间在时间段[95，100]小时的学生人数为0.020×5×200=20（人）．
所以抽取的200位学生中，参加社区服务时间不少于90小时的学生人数为80人．
所以从全市高中学生中任意选取一人，其参加社区服务时间不少于90小时的概率为
$P=\frac{60+20}{200}=\frac{80}{200}=\frac{2}{5}$．
（2）由（1）可知，从全市高中生中任意选取1人，其参加社区服务时间不少于90小时的概率为$\frac{2}{5}$．
由已知得，随机变量ξ的可能取值为0，1，2，3．
所以$P（ξ=0）=C_3^0{（\frac{2}{5}）^0}•{（\frac{3}{5}）^3}=\frac{27}{125}$，
$P（ξ=1）=C_3^1{（\frac{2}{5}）^1}•{（\frac{3}{5}）^2}=\frac{54}{125}$，
$P（ξ=3）=C_3^3{（\frac{2}{5}）^3}•{（\frac{3}{5}）^0}=\frac{8}{125}$．
随机变量ξ的分布列为

ξ	0	1	2	3
P	$\frac{27}{125}$	$\frac{54}{125}$	$\frac{36}{125}$	$\frac{8}{125}$

因为ξ～$B（3，\frac{2}{5}）$，
所以$Eξ=np=3×\frac{2}{5}=\frac{6}{5}$．Dξ=3×$\frac{2}{5}×\frac{3}{5}$=$\frac{18}{25}$．

点评 本题考查概率的求法，考查离散型随机变量的分布列和数学期望的求法，是中档题，解题时要认真审题，注意二项分布的性质的合理运用．