题目内容
已知函数 。
。
(1)求证:不论a为何实数f(x)总是为增函数;
(2)确定a的值,使f(x)为奇函数;
(3)当f(x)为奇函数时,求f(x)的值域。
 。
。(1)求证:不论a为何实数f(x)总是为增函数;
(2)确定a的值,使f(x)为奇函数;
(3)当f(x)为奇函数时,求f(x)的值域。
解:(1)∵f(x)的定义域为R,设x1<x2
则 =
= ,
,
∵x1<x2,
∴ ,
,
∴f(x1)-f(x2)<0
即f(x1)<f(x2),所以不论a为何实数f(x)总为增函数。
(2)∵f(x)为奇函数,
∴f(-x)=-f(x),即 ,
,
解得: .
.
∴ 。
。
(3)由(2)知 ,
,
∵2x+1>1
∴
∴ ,
,
∴
所以f(x)的值域为 。
。
则
 =
= ,
,∵x1<x2,
∴
 ,
,∴f(x1)-f(x2)<0
即f(x1)<f(x2),所以不论a为何实数f(x)总为增函数。
(2)∵f(x)为奇函数,
∴f(-x)=-f(x),即
 ,
,解得:
 .
.∴
 。
。(3)由(2)知
 ,
,∵2x+1>1
∴

∴
 ,
,∴

所以f(x)的值域为
 。
。
练习册系列答案
相关题目





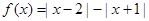 .
. ;
;
 .
. ;
; .
. .
. 在区间
在区间 上存在唯一的极值点,并用二分法求函数取得极值时相应
上存在唯一的极值点,并用二分法求函数取得极值时相应 的近似值(误差不超过
的近似值(误差不超过 );(参考数据
);(参考数据 ,
, ,
, )
) 时,若关于
时,若关于 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围. .
. 在区间
在区间 上存在唯一的极值点,并用二分法求函数取得极值时相应
上存在唯一的极值点,并用二分法求函数取得极值时相应 的近似值(误差不超过
的近似值(误差不超过 );(参考数据
);(参考数据 ,
, ,
, )
) 时,若关于
时,若关于 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.