题目内容
12．已知等差数列{an}的前n项和为Sn，a8=8，S8=36，则数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前100项和为（ ）| A． | $\frac{100}{101}$ | B． | $\frac{99}{101}$ | C． | $\frac{99}{100}$ | D． | $\frac{101}{100}$ |
分析 利用等差数列的通项公式及其前n项和公式、“裂项求和”即可得出．
解答 解：设等差数列{an}的公差为d，∵a8=8，S8=36，
∴$\left\{\begin{array}{l}{{a}_{1}+7d=8}\\{8{a}_{1}+\frac{8×7}{2}d=36}\end{array}\right.$，解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{d=1}\end{array}\right.$，
∴an=1+（n-1）=n．
∴$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{n（n+1）}$=$\frac{1}{n}-\frac{1}{n+1}$．
∴数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前100项和=$（1-\frac{1}{2}）+（\frac{1}{2}-\frac{1}{3}）$+…+$（\frac{1}{100}-\frac{1}{101}）$=1-$\frac{1}{101}$=$\frac{100}{101}$．
故选：A．
点评 本题考查了等差数列的通项公式及其前n项和公式、“裂项求和”，考查了推理能力与计算能力，属于中档题．
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
2．设集合A={x|0＜x＜2015}，B={x|x＜a}．若A⊆B，则实数a的取值范围是（ ）
| A． | {a|a≤0} | B． | {a|0＜a≤2015} | C． | {a|a≥2015} | D． | {a|0＜a＜2015} |
3．若f（x）在[a，b]上连续，则下列说法正确的是（ ）
| A． | f（x）在[a，b]上可导 | |
| B． | ${∫}_{a}^{x}$f（t）dt为f（x）在[a，b]上的一个原函数： | |
| C． | ${∫}_{x}^{b}$f（t）dt为f（x）在[a，b]上的一个原函数 | |
| D． | f（x）在[a，b]上至少有一个零点 |
4．如图，网格纸上小正方形的边长为1，粗线画出的是某个四面体的三视图，则该四面体的表面积为（ ）
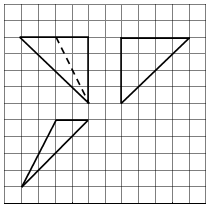
| A． | 8+8$\sqrt{2}$+4$\sqrt{6}$ | B． | 8+8$\sqrt{2}$+2$\sqrt{6}$ | C． | 2+2$\sqrt{2}$+$\sqrt{6}$ | D． | $\frac{1}{2}$+$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{6}}{4}$ |