题目内容
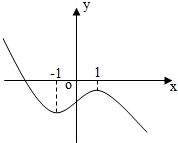 如图,x=±1是函数f(x)=ax3+bx2+cx+d的两个极值点,f'(x)为函数f(x)的导函数,则不等式x•f'(x)>0的解集为
如图,x=±1是函数f(x)=ax3+bx2+cx+d的两个极值点,f'(x)为函数f(x)的导函数,则不等式x•f'(x)>0的解集为(-∞,-1)∪(0,1)
(-∞,-1)∪(0,1)
.分析:根据图象可知(-1,1)时,f'(x)>0;(-∞,-1)或(1,+∞)时,f'(x)<0;再将不等式等价于
或
,从而可解.
|
|
解答:解:由题意,不等式x•f'(x)>0等价于
或
根据图象可知(-1,1)时,f'(x)>0;(-∞,-1)或(1,+∞)时,f'(x)<0;
∴
或
∴0<x<1,或x<-1
故答案为:(-∞,-1)∪(0,1)
|
|
根据图象可知(-1,1)时,f'(x)>0;(-∞,-1)或(1,+∞)时,f'(x)<0;
∴
|
|
∴0<x<1,或x<-1
故答案为:(-∞,-1)∪(0,1)
点评:本题以导函数为载体,考查函数的单调性,考查函数的极值,同时考查了解不等式,关键是从图形中确定函数的单调性.

练习册系列答案
相关题目
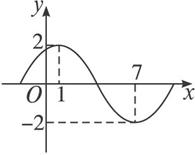
 如图所示的是函数f(x)=Asin(ωx+φ)+B
如图所示的是函数f(x)=Asin(ωx+φ)+B
 如图,x=±1是函数f(x)=ax3+bx2+cx+d的两个极值点,f'(x)为函数f(x)的导函数,则不等式x•f'(x)>0的解集为________.
如图,x=±1是函数f(x)=ax3+bx2+cx+d的两个极值点,f'(x)为函数f(x)的导函数,则不等式x•f'(x)>0的解集为________.