题目内容
 如图所示的是函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|∈(0,
如图所示的是函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|∈(0,| π | 2 |
(1)求函数f(x)的解析式;
(2)求函数f(x)在y轴右侧的第二个对称中心的坐标.
分析:(1)利用函数图象的最大值求出A,求出B,图象经过的特殊点求出φ,利用函数经过(-π,-1)结合ω的范围,求出ω,即可得到函数f(x)的解析式;
(2)求出函数f(x)的对称中心坐标,然后通过k的值求出在y轴右侧的第二个对称中心的坐标.
(2)求出函数f(x)的对称中心坐标,然后通过k的值求出在y轴右侧的第二个对称中心的坐标.
解答:解:(1)由函数的图象可知A=
=2;B=
=1;
将点(0,2)代入得出φ=
;
将点(-π,-1)代入函数 表达式,
可得:2sin[ω(-π)+
]+1=-1
⇒ω(-π)+
=-
+2kπ
⇒ω=
-2k,k∈Z,
又由周期大于2π得ω<1,而且ω>0,所以 ω=
.
∴函数f(x)的解析式:f(x)=2sin(
x+
)+1.
(2)由
x+
=kπ,k∈Z得x=
-
(k∈Z),
∴函数f(x)的对称中心坐标为(
-
,1)(k∈Z);
∴函数f(x)在y轴右侧的第二个对称中心的坐标:(3π-
,1),即(
,1).
| 3-(-1) |
| 2 |
| 3+(-1) |
| 2 |
将点(0,2)代入得出φ=
| π |
| 6 |
将点(-π,-1)代入函数 表达式,
可得:2sin[ω(-π)+
| π |
| 6 |
⇒ω(-π)+
| π |
| 6 |
| π |
| 2 |
⇒ω=
| 2 |
| 3 |
又由周期大于2π得ω<1,而且ω>0,所以 ω=
| 2 |
| 3 |
∴函数f(x)的解析式:f(x)=2sin(
| 2 |
| 3 |
| π |
| 6 |
(2)由
| 2 |
| 3 |
| π |
| 6 |
| 3kπ |
| 2 |
| π |
| 4 |
∴函数f(x)的对称中心坐标为(
| 3kπ |
| 2 |
| π |
| 4 |
∴函数f(x)在y轴右侧的第二个对称中心的坐标:(3π-
| π |
| 4 |
| 11π |
| 4 |
点评:本题考查求y=Asin(ωx+φ)的解析式,条件不管以何种方式给出,一般先求A,再求ω,最后求φ;求y=Asin(ωx+φ)的单调递增区间、对称轴方程、对称中心坐标时,要把ωx+φ看作整体,分别代入正弦函数的单调递增区间、对称轴方程、对称中心坐标分别求出x,利用整体的思想;求y=Asin(ωx+φ)的最大值,需要借助正弦函数的最大值的求解方法即可.

练习册系列答案
相关题目
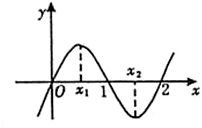
如图所示的是函数f(x)=x3+bx2+cx+d的大致图象,则x12+x22等于( )

A、
| ||
B、
| ||
C、
| ||
D、
|
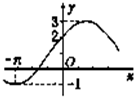 如图所示的是函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|∈(0,
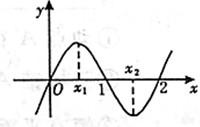
如图所示的是函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|∈(0, 如图所示的是函数f(x)=x3+bx2+cx+d的大致图象,则x12+x22等于( )
如图所示的是函数f(x)=x3+bx2+cx+d的大致图象,则x12+x22等于( )


