题目内容
【题目】在![]() 中,内角
中,内角![]() 所对的边分别为
所对的边分别为![]() ,已知
,已知![]() .
.
(Ⅰ)求角![]() 的值;
的值;
(Ⅱ)记![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(I)已知等式利用正弦定理化简,整理后根据sinA不为0求出cosB的值,即可确定出B的度数;
(II)B=![]() ,可得A+C=
,可得A+C=![]() .
.![]() ∈(-
∈(-![]() ,
,![]() ).令cos
).令cos![]() =t∈(
=t∈(![]() ,1].z=
,1].z=![]() =
=![]() =
=![]() ,利用双勾函数单调性即可得出范围.
,利用双勾函数单调性即可得出范围.
(I)已知等式![]() =
=![]() ,利用正弦定理化简得:
,利用正弦定理化简得:![]() =
=![]() ,
,
即2sinAcosB-sinBcosC=cosBsinC,
可得:2sinAcosB=sinBcosC+sinCcosB=sin(B+C)=sinA,
∵sinA≠0,
∴cosB=![]() ,
,
∵B∈(0,π),
∴B=![]() .
.
(II)因为B=![]() ,所以A+C=
,所以A+C=![]() .所以
.所以![]() ∈(-
∈(-![]() ,
,![]() ).
).
令cos![]() =t∈(
=t∈(![]() ,1].
,1].
z=![]() =
=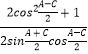 =
=![]() =
=![]() ,
,
可得t=![]() 时,z取得最小值
时,z取得最小值![]() ,
,![]() 时,z取得最大值
时,z取得最大值![]()
∴z的取值范围时![]() .
.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
【题目】在2016年6月英国“脱欧”公投前夕,为了统计该国公民是否有“留欧”意愿,该国某中学数学兴趣小组随机抽查了50名不同年龄层次的公民,调查统计他们是赞成“留欧”还是反对“留欧”.现已得知50人中赞成“留欧”的占60%,统计情况如下表:
年龄层次 | 赞成“留欧” | 反对“留欧” | 合计 |
18岁—19岁 | 6 | ||
50岁及50岁以上 | 10 | ||
合计 | 50 |
(1)请补充完整上述列联表;
(2)请问是否有97.5%的把握认为赞成“留欧”与年龄层次有关?请说明理由.
参考公式与数据: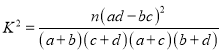 ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |