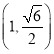题目内容
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)当![]() 时,证明:
时,证明:![]() ;
;
(Ⅲ)求证:对任意正整数![]() ,都有
,都有![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
【答案】(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)见解析
【解析】
(Ⅰ)先求![]() ,再对
,再对![]() 进行讨论即可.
进行讨论即可.
(Ⅱ)由题知即证![]() ,构造新函数设
,构造新函数设![]() ,利用导数
,利用导数![]() 只需
只需![]() 即得证.
即得证.
(Ⅲ)由(Ⅱ)知![]() ,累加作和即得证.
,累加作和即得证.
(Ⅰ)易得,函数![]()
![]() ,
,![]()
![]()
①当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增
上单调递增
②当![]() 时,令
时,令![]() ,解得
,解得![]()
![]() .
.
当![]() 时,
时,![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 上单调递增.
上单调递增.
综上,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(Ⅱ)当![]()
![]() 时,
时,![]() .
.
要证明![]() ,
,
即证![]() ,即
,即![]() . 即
. 即![]() .
.
设![]() 则
则![]()
![]()
令![]() 得,
得,![]() .
.
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() .
.
所以![]() 为极大值点,也为最大值点
为极大值点,也为最大值点
所以![]() .
.
即 .
.
故![]() .
.
(Ⅲ)由(Ⅱ)知,![]() .
.
令![]() ,
,
则 ![]() ,
,
所以![]()
 ,
,
即![]()
所以![]() .
.

练习册系列答案
相关题目
【题目】社会上有人认为在机动车驾驶技术上,男性优于女性,这是真的么?某社会调查机构与交警合作随机统计了经常开车的100名驾驶员最近三个月内是否有交通事故或交通违法事件发生,得到下面的列联表:
男 | 女 | 总计 | |
无 | 40 | 35 | 75 |
有 | 15 | 10 | 25 |
总计 | 55 | 45 | 100 |
附: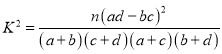
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
据此表,可得( ).
A.认为机动车驾驶技术与性别有关的可靠性不足![]()
B.认为机动车驾驶技术与性别有关的可靠性超过![]()
C.认为机动车驾驶技术与性别有关的可靠性超过![]()
D.认为机动车驾驶技术与性别有关的可靠性超过![]()