题目内容
如图5, 已知抛物线 ,直线
,直线 与抛物线
与抛物线 交于
交于 两点,
两点, ,
, ,
, 与
与 交于点
交于点 .
.
(1) 求点 的轨迹方程;
的轨迹方程;
(2) 求四边形 的面积的最小值.
的面积的最小值.
 |
图5
解法一:
(1)解:设 ,
,
∵ ,
,
∴ 是线段
是线段 的中点.
的中点.
∴ ,①
,①
 . ②
. ②
∵ , ∴
, ∴ .
.
∴ .
.
依题意知 ,
,
∴ . ③
. ③
把②、③代入①得: ,即
,即 .
.
∴点 的轨迹方程为
的轨迹方程为 .
.
(2)解:依题意得四边形 是矩形,
是矩形,
∴四边形 的面积为
的面积为





 .
.
∵ ,当且仅当
,当且仅当 时,等号成立,
时,等号成立,
∴ .
.
∴四边形 的面积的最小值为
的面积的最小值为 .
.
解法二:
(1)解:依题意,知直线 的斜率存在,设直线
的斜率存在,设直线 的斜率为
的斜率为 ,
,
由于 ,则直线
,则直线 的斜率为
的斜率为 .
.
故直线 的方程为
的方程为 ,直线
,直线 的方程为
的方程为 .
.
由 消去
消去 ,得
,得 .
.
解得 或
或 .
.
∴点 的坐标为
的坐标为 .
.
同理得点 的坐标为
的坐标为 .
.
∵ ,
,
∴ 是线段
是线段 的中点.
的中点.
设点 的坐标为
的坐标为 ,
,
则
消去 ,得
,得 .
.
∴点 的轨迹方程为
的轨迹方程为 .
.
(2)解:依题意得四边形 是矩形,
是矩形,
∴四边形 的面积为
的面积为




 .
.
当且仅当 ,即
,即 时,等号成立.
时,等号成立.
∴四边形 的面积的最小值为
的面积的最小值为 . …
. …

 的首项为8,
的首项为8, 是其前n项的和,某同学经计算得S2=20,S3=36,S4=65,后来该同学发现了其中一个数算错了,则该数为 ( )
是其前n项的和,某同学经计算得S2=20,S3=36,S4=65,后来该同学发现了其中一个数算错了,则该数为 ( ) 和
和 分别取一个数,记为
分别取一个数,记为 ,则方程
,则方程 表示焦点在
表示焦点在 轴上且离心率小于
轴上且离心率小于 的椭圆的概率为
的椭圆的概率为 B.
B. C.
C. D.
D.
 的一条弦,点
的一条弦,点 ,
, 交⊙
交⊙ ,若
,若 ,
, ,则
,则
 ,则判断框内的条件是
,则判断框内的条件是 ? B.
? B.  ? C.
? C.  ? D.
? D.  ?
?




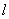 与圆
与圆 (
( 为参数)相交于
为参数)相交于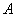 ,
,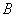 两点,且弦
两点,且弦 的中点坐标是
的中点坐标是 ,则直线
,则直线 上的函数
上的函数 的对称轴为
的对称轴为 ,且当
,且当 时,
时, .若函数
.若函数 (
( )上有零点,则
)上有零点,则 的值为
的值为 或
或 (B)
(B) (C)
(C) 或
或 是虚数单位,那么
是虚数单位,那么 等于 .
等于 .