题目内容
若a>0,b>0且a+b=1,则log2a+log2b的最大值为________.
-2
分析:先把已知条件转化为ab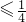 ,且a>0,b>0.再把所求log2a+log2b的最大值转化到ab的最大值表示即可.
,且a>0,b>0.再把所求log2a+log2b的最大值转化到ab的最大值表示即可.
解答:由a>0,b>0且a+b=1得
ab≤ =
= .当且仅当a=b=
.当且仅当a=b= 时取等号.
时取等号.
则log2a+log2b=log2ab≤log2 =-2.
=-2.
则log2a+log2b的最大值为-2.
故答案为-2.
点评:本题是对指数的运算性质,对数的运算性质以及基本不等式的综合考查.考查的都是基本知识点,只要课本知识掌握熟练,是道基础题.
分析:先把已知条件转化为ab
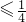 ,且a>0,b>0.再把所求log2a+log2b的最大值转化到ab的最大值表示即可.
,且a>0,b>0.再把所求log2a+log2b的最大值转化到ab的最大值表示即可.解答:由a>0,b>0且a+b=1得
ab≤
 =
= .当且仅当a=b=
.当且仅当a=b= 时取等号.
时取等号.则log2a+log2b=log2ab≤log2
 =-2.
=-2.则log2a+log2b的最大值为-2.
故答案为-2.
点评:本题是对指数的运算性质,对数的运算性质以及基本不等式的综合考查.考查的都是基本知识点,只要课本知识掌握熟练,是道基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
对于使f(x)≤M恒成立的所有常数M中,我们把M的最小值叫做f(x)的上确界.若a>0,b>0且a+b=1,则-
-
的上确界为( )
| 1 |
| 2a |
| 2 |
| b |
A、
| ||
B、-
| ||
C、
| ||
| D、-4 |