题目内容
14.已知球O的半径为R,A,B,C三点在球O的球面上,球心O到平面ABC的距离为$\frac{1}{2}R$,AB=AC=BC=3,则球O的表面积为16π.分析 由已知求出截面圆的半径r,根据已知中球心到平面ABC的距离,根据勾股定理求出球的半径,代入球的表面积公式,即可得到答案.
解答 解:设平面ABC截球所得球的小圆半径为r,则$2r=\frac{3}{sin60°}=2\sqrt{3},r=\sqrt{3}$,
由${R^2}={r^2}+{d^2}={(\sqrt{3})^2}+{(\frac{R}{2})^2}$解得R2=4,所以球的表面积S=4πR2=16π.
故答案为:16π
点评 本题考查的知识点是球的表面积,其中根据球半径,截面圆半径,球心距,构成直角三角形,满足勾股定理,求出球的半径是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.设A={x|x是小于9的正整数},B={3,4,5,6},则∁AB等于( )
| A. | {1,2,3,4,5,6} | B. | {7,8} | C. | {4,5,6,7,8} | D. | {1,2,7,8} |
9.已知a1=1,${a_n}=n({a_{n+1}}-{a_n})(n∈{N^*})$,则数列{an}的通项公式是( )
| A. | n | B. | ${(\frac{n+1}{n})^{n-1}}$ | C. | n2 | D. | 2n-1 |
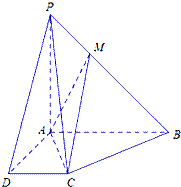 如图所示,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2,M是棱PB上一点.
如图所示,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2,M是棱PB上一点.