题目内容
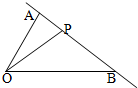 如图,在△AOB中,点P在直线AB上,且满足
如图,在△AOB中,点P在直线AB上,且满足| OP |
| PA |
| OB |
|
| ||
|
|
分析:由
=2t
+t
(t∈R),及A、P、B三点共线,我们不难求出t值,进一步给出向量
与向量
的关系,进而可得答案.
| OP |
| PA |
| OB |
| PA |
| PB |
解答:解:
=
-
,
∴
=2t(
-
)+t
,
得
=
+
.
而P、A、B三点共线,
∴
+
=1,
解得t=1,
∴
=2
+
;
得
-
=2
,
即
=2
,
有
=
.
| PA |
| OA |
| OP |
∴
| OP |
| OA |
| OP |
| OB |
得
| OP |
| 2t |
| 1+2t |
| OA |
| t |
| 1+2t |
| OB |
而P、A、B三点共线,
∴
| 2t |
| 1+2t |
| t |
| 1+2t |
解得t=1,
∴
| OP |
| PA |
| OB |
得
| OP |
| OB |
| PA |
即
| BP |
| PA |
有
|
| ||
|
|
| 1 |
| 2 |
点评:若A、B、P三点共线,O为直线外一点,则
=λ
+μ
,且λ+μ=1,反之也成立,这是三点共线在向量中最常用的证明方法和性质,大家一定要熟练掌握.
| OP |
| OA |
| OB |

练习册系列答案
相关题目
 如图,在△AOB中,
如图,在△AOB中,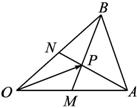
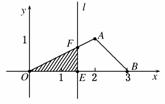
 如图,在△AOB中,点P在直线AB上,且满足
如图,在△AOB中,点P在直线AB上,且满足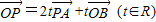 ,求
,求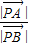 的值.
的值.