题目内容
已知函数

(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)若 ,设
,设 是函数
是函数 的两个极值点,且
的两个极值点,且 ,记
,记 分别为
分别为 的极大值和极小值,令
的极大值和极小值,令 ,求实数
,求实数 的取值范围.
的取值范围.
【答案】
(1) ;
; 时,
时,
 ,
, .(2)
.(2)
【解析】
试题分析:(1)首先求出函数的导数 ,然后求出满足
,然后求出满足 或
或 的区间即可.(2)根据极值点的概念得
的区间即可.(2)根据极值点的概念得 ,在由已知条件求出
,在由已知条件求出 ,极值m,n的表达式,然后整理
,极值m,n的表达式,然后整理 =
=  ,构造函数:令
,构造函数:令 ,通过求导,证明
,通过求导,证明 ,从而可得
,从而可得 即可.
即可.
试题解析:(1)  ,
2分 令
,
2分 令 ,
, 
①.
②. 时,
时, ,令
,令
 ,
, 6分
6分
(2)依题意有

 , 9分
, 9分
令 ,
,

 13分
13分
考点:1.求函数的导数和导数的性质;2.导数的极值和导数性质的应用.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
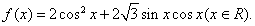
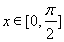
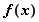

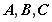
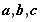
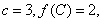
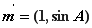
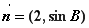
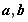

 时,求函数的最大值和最小值;
时,求函数的最大值和最小值; 的取值范围,使
的取值范围,使 在区间
在区间 上是单调减函数
上是单调减函数 .(
.( ).
). 时,求函数
时,求函数 的极值;
的极值; (2)若对
(2)若对 ,有成立,求实数
,有成立,求实数 的取值范围.
的取值范围.
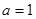 时,求
时,求 的极小值;
的极小值; ,求
,求 的最大值
的最大值 .
.