题目内容
(15分) 如图,已知点P在圆柱OO1的底面⊙O上,AB、A1B1分别为⊙O、⊙O1的直径,且A1A⊥平面PAB.
(1)求证:BP⊥A1P;
(2)若圆柱OO1的体积V=12π,OA=2,∠AOP=120°,求三棱锥A1-APB的体积.
(3)在AP上是否存在一点M,使异面直线OM与A1B所成角的余弦值为
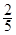 ?若存在,请指出M的位置,并证明;若不存在,请说明理由.
?若存在,请指出M的位置,并证明;若不存在,请说明理由.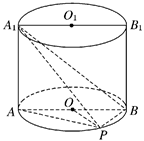
(1)证明:因为AP⊥BP,由AA1⊥平面PAB,得AA1⊥BP
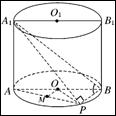
且AP∩AA1=A
; 所以BP⊥平面PAA1
故BP⊥A1P
(2)由题意V=π·OA2·AA1=4π·AA1=12π,解得AA1=3
由OA=2,∠AOP=120°,得∠BAP=30°,BP=2
AP=2,∴S△PAB=×2×2=2
∴三棱锥A1-APB的体积V=S△PAB·AA1=×2×3=2
(3)答:在AP上存在一点M,当M为AP的中点时,使异面直线OM与A1B所成角的余弦值为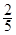
证明:∵O、M分别为AB、AP的中点,则OM∥BP,且已证BP⊥A1P
∴∠A1BP就是异面直线OM与A1B所成的角
在Rt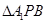 中,
中,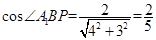
∴在AP上存在一点M,当M为AP的中点时,使异面直线OM与A1B所成角的余弦值为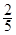

且AP∩AA1=A
; 所以BP⊥平面PAA1
故BP⊥A1P
(2)由题意V=π·OA2·AA1=4π·AA1=12π,解得AA1=3
由OA=2,∠AOP=120°,得∠BAP=30°,BP=2
AP=2,∴S△PAB=×2×2=2
∴三棱锥A1-APB的体积V=S△PAB·AA1=×2×3=2
(3)答:在AP上存在一点M,当M为AP的中点时,使异面直线OM与A1B所成角的余弦值为
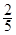
证明:∵O、M分别为AB、AP的中点,则OM∥BP,且已证BP⊥A1P
∴∠A1BP就是异面直线OM与A1B所成的角
在Rt
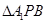 中,
中,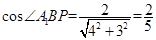
∴在AP上存在一点M,当M为AP的中点时,使异面直线OM与A1B所成角的余弦值为
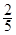

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 B 1∶3 C 1∶3
B 1∶3 C 1∶3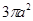
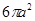
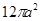
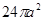
 BCD中,
BCD中,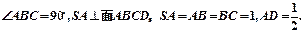
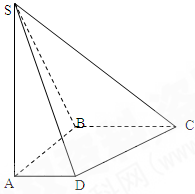
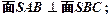
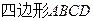 是边长为1的正方形,则该几何体的体积为( )
是边长为1的正方形,则该几何体的体积为( )
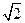



 的一个正方体,其全面积与球
的一个正方体,其全面积与球 的表面积相等,则球
的表面积相等,则球 30°的二面角,则此截面的面积为( )
30°的二面角,则此截面的面积为( )
 2
2
 的表面积为
的表面积为 ,
, 是球面上的三点,点
是球面上的三点,点 是
是 的中点,
的中点,

 ,则二面角
,则二面角 的大小为
的大小为