题目内容
已知数列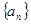 的前
的前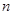 项和为
项和为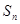 ,若
,若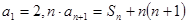 ,
,
⑴证明数列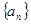 为等差数列,并求其通项公式;
为等差数列,并求其通项公式;
⑵令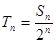 ,①当
,①当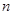 为何正整数值时,
为何正整数值时,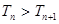 :②若对一切正整数
:②若对一切正整数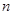 ,总有
,总有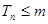 ,求
,求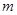 的取值范围.
的取值范围.
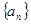 的前
的前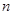 项和为
项和为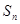 ,若
,若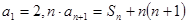 ,
,⑴证明数列
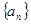 为等差数列,并求其通项公式;
为等差数列,并求其通项公式;⑵令
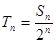 ,①当
,①当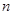 为何正整数值时,
为何正整数值时,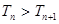 :②若对一切正整数
:②若对一切正整数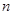 ,总有
,总有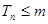 ,求
,求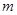 的取值范围.
的取值范围.(1)证明详见解析,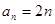 ;(2)①
;(2)①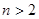 ,②
,②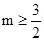 .
.
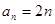 ;(2)①
;(2)①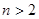 ,②
,②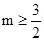 .
.试题分析:(1)关于
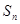 和
和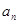 的递推式,一般有两种方法可解决,1:转化为项的递推式,根据递推式 直接求通项公式,2:转化为
的递推式,一般有两种方法可解决,1:转化为项的递推式,根据递推式 直接求通项公式,2:转化为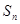 的递推关系,先求
的递推关系,先求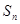 ,再求通项公式,该题已知数列前n项和
,再求通项公式,该题已知数列前n项和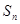 和
和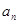 的递推关系,由
的递推关系,由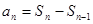 可的
可的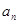 与
与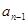 的关系,然后由等差数列定义证明,知道等差数列后再求通项公式;
的关系,然后由等差数列定义证明,知道等差数列后再求通项公式;(2)①将
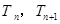 代入不等式,解不等式可得,②恒成立问题往往可以采取参变分离的方法,
代入不等式,解不等式可得,②恒成立问题往往可以采取参变分离的方法,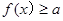 或
或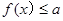 的形式,最后转化为求函数
的形式,最后转化为求函数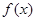 最值,即
最值,即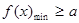 或
或 ,该题可转化为求
,该题可转化为求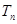 的最大值问题,求
的最大值问题,求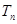 的最大值可以结合函数的函数或者单调性处理,但是注意定义域
的最大值可以结合函数的函数或者单调性处理,但是注意定义域 .
.试题解析:(1)令
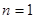 ,
,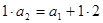 ,即
,即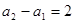 ,由
,由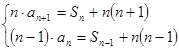

∵
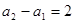 ,∴
,∴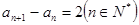 ,
,即数列
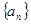 是以2为首项,2为公差的等差数列, ∴
是以2为首项,2为公差的等差数列, ∴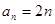
(2)①
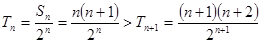 ,即
,即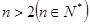 ②∵
②∵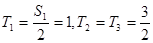 ,又∵
,又∵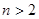 时,
时,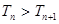
∴各项中数值最大为
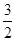 ,∵对一切正整数
,∵对一切正整数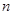 ,总有
,总有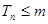 恒成立,因此
恒成立,因此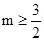 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
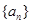 是公比大于1的等比数列,
是公比大于1的等比数列,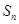 为其前
为其前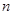 项和已知
项和已知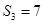 ,且
,且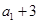 ,
,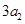 ,
,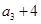 构成等差数列.
构成等差数列.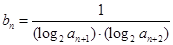 ,求数列
,求数列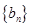 的前
的前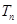 .
.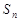 是等差数列
是等差数列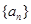 的前n项和,已知
的前n项和,已知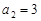 ,
,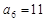 ,则
,则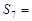 .
.
 中,
中, ,则前13项之和等于( )
,则前13项之和等于( )



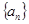 满足
满足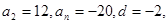 则
则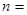 ( )
( )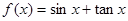 .项数为27的等差数列
.项数为27的等差数列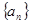 满足
满足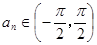 ,且公差
,且公差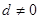 .若
.若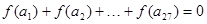 ,则当
,则当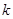 =____________时,
=____________时,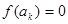 .
. 为等差数列
为等差数列 的前n项和,若
的前n项和,若 ,则
,则 = .
= .