题目内容
已知等比数列 中,公比
中,公比 若
若 则
则 有( )
有( )
 中,公比
中,公比 若
若 则
则 有( )
有( )| A.最小值-4 | B.最大值-4 | C.最小值12 | D.最大值12 |
C
试题分析:因为等比数列
 中,公比
中,公比 若
若 所以,
所以, ,
, =
= ,当且仅当q=1时,
,当且仅当q=1时, 有最小值12,故选C。
有最小值12,故选C。点评:小综合题,根据已知条件,得到q的函数式,应用均值定理求得最值。应用均值定理应注意“一正、二定、三相等”。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
 满足
满足
 ,记
,记 ,证明:
,证明: 。
。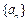 是以a为首项,q为公比的等比数列,
是以a为首项,q为公比的等比数列,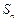 为它的前n项和.
为它的前n项和.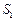 、
、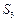 、
、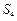 成等差数列时,求q的值;
成等差数列时,求q的值;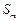 、
、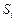 成等差数列时,求证:对任意自然数k,
成等差数列时,求证:对任意自然数k,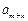 、
、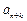 、
、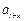 也成等差数列.
也成等差数列.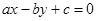 被曲线
被曲线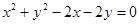 截得的弦长的最小值为
截得的弦长的最小值为


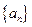 满足
满足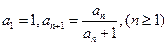 ,数列
,数列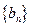 满足
满足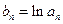 ,数列
,数列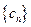
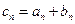 .
.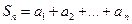 ,
,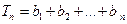 ,试比较
,试比较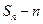 与
与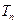 的大小,并证明;
的大小,并证明;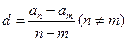 是一个常数,显然在本题的数列
是一个常数,显然在本题的数列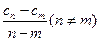 不是一个常数,但
不是一个常数,但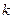 呢,若会,请求出
呢,若会,请求出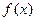 、
、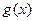 对任意实数
对任意实数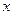 、
、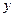 都满足条件
都满足条件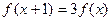 ,且
,且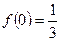 ,和②
,和②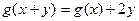 ,且
,且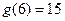 ,
,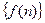 、
、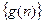 的通项公式;(
的通项公式;(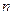 为正整数)
为正整数)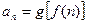 ,求数列
,求数列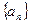 的前
的前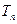 。
。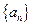 是各项不为0的等差数列,
是各项不为0的等差数列,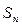 为其前n
为其前n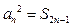 , 令
, 令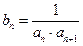 ,数列
,数列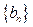 的
的
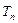 .
.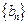 的前n项和
的前n项和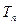 ;
;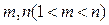 ,使得
,使得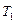 ,
,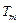 ,
,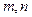 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. ,
, 为实数,首项为
为实数,首项为 的前
的前 项和为
项和为 ,满足
,满足 .
. , 求
, 求 及
及 14分)已知数列
14分)已知数列 是以
是以 d为公差的等差数列,数列
d为公差的等差数列,数列 是以q为公比的
是以q为公比的 且
且 ,求整数q的值;
,求整数q的值; ,使得
,使得 项的和?请说明理由;
项的和?请说明理由; ,求证:数列
,求证:数列