Question

【题目】已知函数

（1）证明：在上单调递减；

（2）已知在单调递增，记函数的最小值为.

①求的表达式；

②求的最大值.

Answer 1

【答案】（1）见解析；（2）①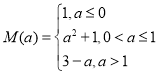；②2.

【解析】

（1）直接利用单调性的定义证明；

（2）①先求得函数在时的最小值，再看当时，函数的最小值，只需对a讨论，借助于二次函数的单调性求得答案．

②直接由解析式得解.

（1）任取x1，x2∈（0，1），设x1＜x2，则

f（x1）﹣f（x2）＝

．

∵0＜x1＜x2＜1，∴，∴＜2，

∴0，即f（x1）﹣f（x2）>0，

∴f（x1）＞f（x2）．

∴函数f（x）在（0，1）上单调递减；

（2）①∵在单调递增，∴函数在时满足在（0，1）上单调递减，在单调递增，此时在时的最小值为，

当时，对称轴为，

当时，二次函数开口向上，；

当a＞0时，函数在时单调递减，函数在时．

当时，即a>1时，，

当<a≤时，，

综上，；

②由，可得当a=1时，函数有最大值为.